Условная вероятность. Теоремы умножения вероятностей

Определение 1. События 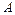и называются независимыми, если появление одного из них при первом испытании не влияет на вероятность появления другого события при следующем испытании.

Пример: подбрасывание двух монет («герб - решка»).

Определение 2. События А и В называются зависимыми, если появление одного из них при первом испытании влияет на вероятность появления другого события при следующем испытании.

Пример: в ящике 4 бракованных и 8 стандартных деталей, которые достают из ящика случайным образом без возврата назад. Появление стандартной детали при первом испытании влияет на вероятность появления стандартной детали при втором испытании, то есть эти два события являются зависимыми.

Определение 3. Если вероятность события 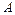вычисляется при условии, что событие уже произошло, то такая вероятность называется условной и обозначается

или .

, .

Теорема 1. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже произошло:

,

.

Теорема 2. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий

.

Пример 1. Три стрелка сделали по одном выстрелу в одну и ту же мишень. Вероятность попадания каждого из них соответственно равна: 0,6; 0,7; 0,9. Найти вероятность того, что попадут в мишень 2 стрелка.

Решение. Пусть события — попадание соответственно 1-го, 2-го и 3-го стрелка.

Тогда 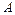— событие, когда попадут 2 стрелкаа, представим таким способом:

.

Тогда:

.