Метод LU - розкладання

Розв’язання системи лінійних рівнянь алгебраїчних рівнянь за допомогою методу LU – розкладання зводиться до наступного. Нехай задана система

. (36)

Представимо матрицю у вигляді добутку двох матриць і :

,

де елементи 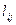і 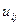обчислюються за формулами:

(37)

(38)

Формули (37) і (38) дають нам LU – розкладання матриці А. Таким чином, якщо 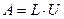, то можна записати рівняння еквівалентне (36):

, (39)

Яке можна представити у вигляді системи

(40)

де – деякий допоміжний вектор.

Таким чином, розв’язання системи з квадратною матрицею зводиться до розв’язання двох систем з трикутними матрицями коефіцієнтів:

(41)

і

(42)

Із (35) і (36) зрозуміло, що всі і 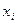можуть бути обчислені за формулами:

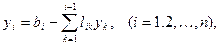(43)

. (44)

Приклад 2. Розв’язати систему лінійних рівнянь методом Гаусса з використанням стандартної процедури пакетe Mathcad

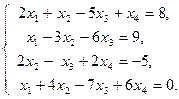
Розв’язання систему лінійних рівнянь методом Гаусса з використанням стандартної процедури пакету Mathcad 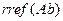виконується за наступним алгоритмом:

1. Сформувати матрицю коефіцієнтів і вектор вільних членів заданої системи.

2. Сформувати розширену матрицю системи за допомогою процедури .

3. За допомогою процедури 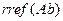, звести розширену матрицю до східчастого вигляду.

4. Дістати розв’язок системи, виділивши останній стовпець матриці, одержаної в попередньому пункті.

5. Виконати перевірку, виконавши обчислення матричного виразу.