Основні поняття. 1 Название, цель, содержание работы

Основні поняття

Система алгебраїчних рівнянь називається лінійною, якщо вона може бути записана у вигляді:

(1)

або

,

де – невідомі; 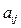– дійсні числа, які називають коефіцієнтами системи; – вільні члени.

Систему лінійних алгебраїчних рівнянь часто записують у матричній формі

(2)

, , ,

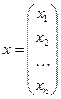де А – матриця коефіцієнтів системи, 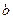– вектор вільних членів і 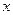– вектор невідомих. Матриця з вимірності називається прямокутною. У випадку, якщо , то матрицю називають квадратною матрицею порядку .

Квадратна матриця вимірності називається:

ð нульовою, якщо всі елементи дорівнюють нулю: ;

ð верхньою трикутною, якщо всі елементи, розташовані нижче головної діагоналі, дорівнюють нулю: ;

ð нижньою трикутною, якщо всі елементи, розташовані вище головної діагоналі, дорівнюють нулю: ;

ð діагональною, якщо всі елементи, крім головної діагоналі, дорівнюють нулю: ;

ð одиничною, якщо всі елементи головної діагоналі дорівнюють одиниці, а всі інші – нулю: .

Квадратна матриця називається неособливою, якщо її визначник (детермінант) відмінний від нуля. У протилежному випадку матриця називається особливою або виродженою.

Якщо матриця А неособлива, тобто її визначник не дорівнює нулю, то система (2) має єдиний розв’язок. У лінійній алгебрі звичайно використовують спосіб розв’язання системи рівнянь (2), який базується на обчислені оберненої матриці . Дійсно, якщо помножити обидві частини рівняння (2) на , розв’язок рівняння (2) отримаємо у вигляді

. (3)

Як відомо, елементи оберненої матриці можна обчислити за відомою формулою , де – алгебраїчні доповнення елемента матриці А і визначник цієї матриці. Тоді для знаходження всіх її елементів потрібно обчислити визначників ­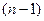-го порядку. Остання задача настільки трудомістка (вимагає велику кількість арифметичних операцій), що розв’язати її навіть при дуже важко (це задача складності ).

Менш трудомістким є метод Крамера, згідно з яким значення невідомих знаходяться за допомогою формули

, (4)

де матриця 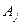формується з матриці 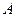заміною її j -го стовпця на стовпець вільних членів. Але для розв’язання системи лінійних алгебраїчних рівнянь з невідомими у такий спосіб потрібно обчислити визначник порядку , що знову ж таки вимагає виконання арифметичних операцій порядку 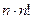. Уже при , такий обсяг обчислень практично не доступний сучасним комп’ютерам. Тому далі ми будемо розглядати більш ефективні для обчислень методи.

У зв’язку з цим наведемо визначення деяких спеціальних матриць. Квадратна матриця 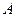називається:

ð симетричною, якщо ;

ð кососиметричною, якщо ;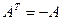

ð ортогональною, якщо і ;

ð ідемпотентною, якщо ;

ð інволютивною, якщо , де Е – одинична матриця.

Методи чисельного розв’язання систем рівнянь (2) діляться на дві групи: прямі та ітераційні. До першої групи належать наведені вище методи розв’язання систем лінійних алгебраїчних рівнянь. В прямих або точних методах кількість арифметичних операцій, потрібних для отримання розв’язку 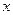системи (2) є скінченим числом, причому, якщо обчислення виконуються точно (без заокруглень), то розв’язок отримуємо точний. Прикладом прямого методу є також метод Гаусса та його модифікації. Ітераційні методи полягають в тому, що розв’язок 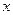системи (2) знаходять як границю послідовних наближень , коли , де – номер ітерації.

Чисельні методи розв’язання задач лінійних алгебри на сьогодні добре досліджені та описані в літературі. Крім того, є розроблено ряд математичних пакетів (Mathcad, Mathematica, Maple, Matlab), які дають можливість як досліджувати, так і розв’язувати задачі лінійної алгебри. Для ілюстрації обчислень і викладок ми вибрали пакет Mathcad з огляду на можливість виконувати за допомогою цього пакету арифметичні операції як в символьному, так і в числовому вигляді. А наявність нотації запису формул близької до звичайних математичних записів, на нашу думку, буде сприяти кращому розумінню та засвоєнню алгоритмів розв’язання задач лінійної алгебри. Цьому ж буде сприяти і наявність простих засобів програмування та можливостей графічного редактора даного пакету.