Умови застосування методу Гаусса

Все сказане вище можна перенести і на системи рівнянь довільного порядку. В такому випадку процес вилучення можна записати за допомогою формули

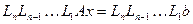, (30)

де елементарна нижня трикутна матриця 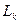на k -му кроці має вигляд

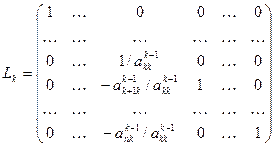. (31)

Очевидно, що матриці 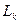існують, коли 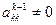для кожного 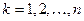. Остання умова буде виконана, якщо усі кутові мінори матриці А відмінні від нуля. Нагадаємо, що кутові мінори матриці А мають вигляд:

.

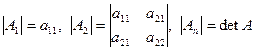Матриці і 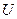у випадку системи n -го порядку мають вигляд:

, .

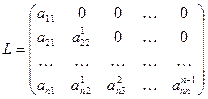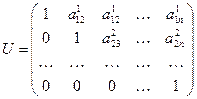Запис методу Гаусса у вигляді (30) детально описує процес виключення. Тепер його можна реалізувати інакше. Нехай задані матриця 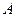і вектор 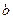. Спочатку проводиться розкладання 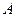на добуток двох трикутних матриць 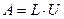. Тоді початкова система набуває вигляду 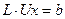, а її розв’язання рівносильно послідовному розв’язанню систем рівнянь:

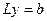, (32)

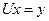(33)

з трикутними матрицями, звідки й знаходиться шуканий вектор 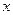за допомогою наступних алгоритмів:

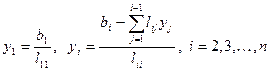; (34)

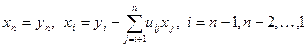, (35)

де 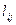і 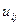елементи матриць і 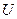, відповідно.

Розглянутий вище алгоритм (30) зведення системи рівнянь до системи з верхньою трикутною матрицею ефективно реалізовується на паралельних процесорах.