Метод вилучення Гаусса

Найпростішим варіантом методу вилучення Гаусса є схема єдиного ділення. Відповідно до даної схеми алгоритм виключення невідомої 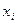і -те рівняння , яке називається головним, ділять на провідний коефіцієнт . Потім отримане таким чином рівняння множать на і віднімають відповідно із -го, -го, і т.д, -го рядків системи (1). В результаті таких перетворень, при умові, що визначник матриці системи не дорівнює нулю, приходимо до системи з трикутною матрицею з одиничними діагональними елементами, яка є еквівалентна вихідній системі. Якщо провідний елемент на і -му кроці перетворюється в нуль , то для продовження процесу, у відповідній системі і -й рядок потрібно поміняти місцями з одним із наступних рядків. Остаточно розв’язок системи одержується шляхом розв’язання одержаної системи з трикутною матрицею, що уже не складає труднощів.

Розглянемо цей алгоритм детальніше. Нехай маємо систему рівнянь з невідомими (1).

Будемо реалізовувати метод Гаусса шляхом еквівалентних перетворень системи. Для зручності записів введемо позначення: , , .

Тоді системи (1) запишемо у вигляді

(5)

Метод виключення Гаусса, прийнято реалізовувати за два ходи: прямого і зворотного. На прямому ході, за допомогою еквівалентних перетворень, систему (5) зводять до верхнього трикутного вигляду, а на зворотному ході, з одержаної системи знаходять, значення невідомих, тобто розв’язок системи.

Прямий хід методу Гаусса. Нехай . Тоді перше рівняння залишимо без зміни

(6)

і використаємо його для виключення невідомого із всіх рівнянь системи (5), починаючи з другого. Для виключення із другого рівняння додамо до нього перше, помножене на . Потім, помноживши перше рівння на і додамо результа до третього рівняння, також виключимо з нього і т.д. В результаті одержимо системи рівнянь вигляду

(7)

де .

Нехай . Тоді друге рівняння залишимо без зміни

, (8)

і використаємо його для виключення невідомого 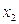із всіх рівнянь системи (5), починаючи з третього. Для цього до третього і наступних рівняннь системи (7) додамо рівняння (8), помножене на 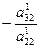. В результаті одержимо систему вигляду

(9)

де

Продовжуючи процес за даною схемою далі, на n- 1 - му кроці одержимо систему трикутного вигляду

(10)

На цьому закінчується прямий хід методу Гаусса.

Зворотний хід. На зворотному ході методу Гаусса знаходимо значення невідомих в оберненому порядку.

З останнього рівняння системи (10) маємо, що . Тоді з передостаннього рівняння системи (10) знаходимо: т.д. Нарешті з першого рівняння знаходимо: .

У загальному випадку під час прямого ходу методу Гаусса коефіцієнти системи та праві частини обчислюються за наведеними нижче формулами:

;

(11)

(12)

(13)

. (14)

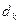Якщо коефіцієнти і праві частини зберігаються в пам’яті ЕОМ, то зворотний хід здійснюється за формулами:

або . (15)

Основним обмеженням методу Гаусса є припущення про те, що всі ведучі елементи відмінні від нуля. Слід мати на увазі, що якщо якийсь ведучий елемент не дорівнює нулю, а просто близький до нього, то в процесі обчислень може відбутись значне накопичення похибок. У такому разі, як уже відмічалось, у відповідній системі достатньо буде переставити місцями (перенумерувати) рівняння для продовження процесу вилучення. Уникнути цього дозволяє метод Гаусса з вибором головного елемента.

Ідея методу Гаусса з вибором головного елемента полягає в тому, щоб на черговому кроці виключати ту невідому, коефіцієнт при якій найбільший за модулем. Отже, ведучим елементом тут вибирається найбільший за модулем елемент матриці. Тим самим, якщо , то в процесі обчислень не відбудеться ділення на нуль.

На практиці, для зменшення похибок заокруглення, здебільшого, роблять так. Серед елементів першого стовпця кожної проміжної матриці з номером вибирають найбільший за модулем елемент в і-му стовпці і роблять його ведучим, проводячи при цьому перестановка і-го і -го рівнянь. Такий спосіб виключення називається методом Гаусса з вибором головного елемента за стовпцем. Він еквівалентний застосуванню звичайного методу Гаусса до системи, в якій на кожному кроці виключення робиться відповідна перестановка рівнянь.

Підрахунок числа операцій множення і ділення. Визначимо складність алгоритму, що реалізує метод Гаусса на однопроцесорній ЕОМ. Оскільки виконання операцій множення і ділення на ЕОМ вимагає значно більше часу, ніж виконання додавання і віднімання, то обмежимось підрахунком числа множень і ділень.

1. Обчислення коефіцієнтів , за формулою (11) потребує

ділень.

2. Обчислення усіх коефіцієнтів за формулою (12) вимагає множень

.

Таким чином обчислення не нульових елементів матриці (10) вимагає

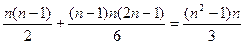
множень і ділень. При великих це число дій наближено рівне .

3. Обчислення правих частин 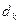за формулою (14) потребує

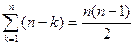
операцій множення. Отже, обчислення правих частин перетвореної системи (10) вимагає

дій множення і ділення.

Разом для здійснення прямого ходу методом Гаусса необхідно виконати

, (16)

дій із яких, основне число дій (порядку ) приходиться на обчислення коефіцієнтів матриці системи (10).

4. Для здійснення зворотного ходу методу Гауса за формулами (15) потребує

(17)

множень.

Таким чином, для реалізації методу Гаусса потрібно виконати

(18)

операцій множення і ділення.

На основі одержаних результатів можна зробити висновок, що за затратами часу і необхідної машинної пам’яті метод Гаусса придатний для розв’язання системи рівнянь (5) загального вигляду з числом невідомих порядку 100.

Нижче наведено приклад покрокової реалізації алгоритму методу Гаусса (прямий і зворотний хід), на основі якого одержано формули для підрахунку числа операцій множення і ділення і підраховано їх кількість при .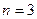

В табл. 1 наведено число множень і ділень при різних значеннях .

Таблиця 1

n
N

На лістингу 2 наведено програму, яка реалізовує метод Гаусса з вибором головного елемента по стовпцях, що запобігає і діленню на ведучий елемент рівний нулю. Це проілюстровано в першому прикладі.