Квадратная матрица и ее определитель. Особенная и неособенная квадратные матрицы. Присоединенная матрица. Матрица, обратная данной, и алгоритм ее вычисления

Квадратная матрица и ее определитель. Особенная и неособенная квадратные матрицы. Присоединенная матрица. Матрица, обратная данной, и алгоритм ее вычисления.

Невырожденные (неособенные) матрицы:

Вырожденные (особенные) матрицы:

Присоединенной матрицей 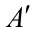матрицы называется матрица, элементами которой являются алгебраические дополнения элементов транспонированной матрицы .

Пусть А – квадратная матрица, Е – единичная матрица того же размера. Матрица В называется обратной к матрице А, если АВ = Е и В ∙ А = Е.

Обратная матрица обозначается А^-1.

АА^-1 = А^-1А = Е

Теорема 2. Квадратная матрица А имеет обратную тогда и только тогда, когда её определитель │А│ отличен от нуля.

Доказательство: если А имеет обратную, то Е = А ∙ А^-1, откуда по свойству 10 определителей имеем

1 = │Е│ = │ А ∙ А^-1│= │А│ ∙ │А^-1│, откуда видно, что │А│≠ 0.

Алгоритм построения обратной матрицы:

1) вычислить │А│. Если │А│= 0, то по доказательству А^-1 не существует. На этом вычисления заканчиваются. переходим к следующему этапу.

2) выписать транспонированную матрицу А'.

3) составляем матрицу , составленную из алгебраических дополнений элементов матрицы А'. Матрица называется присоединённой к матрице А.

4) выписываем ответ по формуле А^-1 = .

5) делаем проверку: проверяем равенства А ∙ А^-1 = Е и А^-1 ∙ А = Е.

4. Понятие минора k- го порядка. Ранг матрицы (определение). Вычисление ранга матрицы с помощью элементарных преобразований. Пример.

Рассмотрим матрицу А размером mxn. Выделим в матрице любые k строк и k столбцов. Элементы, стоящие на пересечении этих строк и столбцов, образуют определитель k-го порядка. Его называют минором матрицы А порядка k.

Рангом матрицы А называется наибольший порядок отличного от нуля минора этой матрицы.

Иными словами, число r называется рангом ненулевой матрицы А, если:

1) у матрицы А есть ненулевой минор порядка r;

2) всякий минор порядка (r+1) и выше равен нулю.

Ранг матрицы А обозначается символом rangA.

Матрицу называют ступенчатой, если каждая её строка начинается со строго большего числа нулей, чем предыдущий.

Теорема 1. Ранг ступенчатой матрицы равен числу ненулевых строк в ней.

Обратная матрица и её нахождение методом присоединённой матрицы

Пусть А – квадратная матрица, Е – единичная матрица того же размера. Матрица В называется обратной к матрице А, если АВ = Е и В ∙ А = Е.

Обратная матрица обозначается А^-1.

АА^-1 = А^-1А = Е

Теорема 2. Квадратная матрица А имеет обратную тогда и только тогда, когда её определитель │А│ отличен от нуля.

Доказательство: если А имеет обратную, то Е = А ∙ А^-1, откуда по свойству 10 определителей имеем

1 = │Е│ = │ А ∙ А^-1│= │А│ ∙ │А^-1│, откуда видно, что │А│≠ 0.