 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Абсолютные и средние показатели вариации и способы их расчета
|
|
Размах вариации R = Xmax – Xmin устанавливает только крайние отклонения, то есть пределы выборки.
Среднее абсолютное линейное отклонение 
учитывает различия всех единиц изучаемой совокупности
Средний квадрат отклонений (дисперсия)  . Расчет дисперсии можно производить по формуле:
. Расчет дисперсии можно производить по формуле: 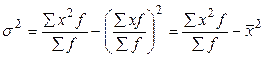
Среднее квадратичное отклонение  . Чем меньше среднее квадратичное отклонение, тем лучше средняя величина отражает собой всю представленную совокупность. Между средним абсолютным и средним квадратичным отклонением существует соотношение
. Чем меньше среднее квадратичное отклонение, тем лучше средняя величина отражает собой всю представленную совокупность. Между средним абсолютным и средним квадратичным отклонением существует соотношение 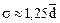 .
.
Свойства дисперсии.
| 1. Уменьшение всех значений признака на одну и ту же величину не меняет величины дисперсии | 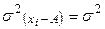
|
| 2. Уменьшение всех значений признака в k раз уменьшает дисперсию в k2 | 
|
| 3. Дисперсия от средней меньше дисперсии, исчисленной от любой величины А | 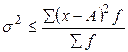
|
Альтернативный признак. Обозначим 1 – наличие признака; 0 – отсутствие; p – долю единиц, обладающих данным признаком; q – долю единиц, не обладающих данным признаком (p+q=1).
Среднее значение альтернативного признака 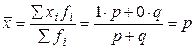
Дата публикования: 2014-11-18; Прочитано: 497 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
