Структурные средние величины

Для характеристики структуры совокупности применяются структурные средние: мода и медиана.

Модой (Мо) называется наиболее часто встречающееся или типичное значение признака, т.е. то значение варианты, которое соответствует максимальной точке теоретической кривой распределения вариационного ряда. Мода часто используется при изучении покупательского спроса.

В дискретном ряду мода – это варианта с наибольшей частотой. В интервальном ряду мода – центральный вариант модального интервала, то есть того интервала, который имеет наибольшую частоту (частость). В пределах интервала находят значение признака, которое является модой по формуле

,

где: 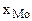– нижняя граница модального интервала; – величина модального интервала; – частота, соответствующая модальному интервалу; 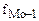– частота, предшествующая модальной; – частота интервала, следующего за модальным.

Пример 3. Дан дискретный ряд распределения купленных пар обуви

Размер обуви
Число купленных пар				88 Мо

Определим значение моды. Варианта с наибольшей частотой равна 88. Этой частоте соответствует варианта, значение которой Мо = 37 размер.

Пример 4. Дан интервальный ряд распределения числа рабочих по стажу работы.

Стаж (лет) Число рабочих До 2 2-4 4-6 6-8 8-10 свыше 10

Модальным интервалом является интервал 6-8 соответствующий наибольшей частоте равной 35. Значение моды находится внутри этого интервала.

лет.

Медиана (Ме) – это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньшие, чем средний вариант, а другая – большие.

– для четного ряда.

Для ранжированного ряда с нечетным числом членов медианой является варианта, расположенная в центре ряда.

Для ранжированного ряда с четным числом членов ряда медианой будет среднее арифметическое из двух смежных вариант.

В интервальном ряде

где: 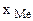– нижняя граница медианного интервала; – величина медианного интервала; – полусумма частот ряда; – сумма накопленных частот, предшествующих медианному интервалу; – число наблюдений (частота) медианного интервала.

Свойство медианы: сумма абсолютных отклонений членов ряда от медианы минимальна .

Пример 5. Имеются данные о расположении магазинов от базы. Вычислить отклонения от среднего и медианных значений.

№	Расположение магазина от базы, км (х)	Отклонение от среднего значения,	Отклонение от медианного значения,
Итого

Среднее значение км. Медианой нечетного ряда является центральный вариант, находящийся на 3-ем месте, равный Ме = 4 км.

Пример 6. Рассчитать среднюю заработную плату в целом по трем предприятиям в зависимости от имеющихся данных

Предприятие	Численность персонала, чел.	Месячный ФЗП, тыс. руб.,	Средняя заработная плата,
А
		564,84 332,75 517,54
Итого		1415,13

Среднюю заработную плату рассчитаем разными способами в зависимости от того, какие данные нам будут известны.

1. Если имеются данные групп 1 и 2, формула средней агрегатной

руб.,

где: ; – вариант определяемого признака; – вес i-го варианта.

2. Если есть данные групп 1 и 3, то общая средняя может быть рассчитана по формуле средней арифметической взвешенной

руб.

3. Если имеются данные 3 группы, а частоты равны между собой или отсутствуют, то используются формула средней арифметической простой

руб.

4. Если имеются данные групп 2 и 3, то расчет ведется по средней гармонической взвешенной

руб.

Задача 1. Имеются следующие данные о заработной плате рабочих участка. Определить среднюю заработную плату рабочих участка.

Профессия	Количество рабочих	Заработная плата каждого рабочего участка за месяц, руб.
Токари Фрезеровщики Слесари		1700, 1208, 917, 1620, 1400 1810, 1550 1210, 1380, 870

Решение. Воспользуемся формулой простой средней арифметической

Задача 2. Распределение рабочих по стажу работы следующее. Определить средний стаж работы рабочих участка.

Стаж рабочих, лет	до 5 лет	5 - 10	10 - 15	15 и более
Количество рабочих, f
Серединное значение интервала, x	2,5	7,5	12,5	17,5

Решение. Воспользуемся формулой расчета средней арифметической взвешенной для интервального ряда. Предварительно вычислим серединное значение интервального признака х, дополнив открытые интервалы значениями недостающих границ:

Средний стаж рабочих участка

лет

Задача 3. Имеются следующие данные об экспорте продукции металлургического комбината. Определить средний удельный вес продукции на экспорт.

Вид продукции	Удельный вес Продукции на экспорт, % х	Стоимость продукции на экспорт, тыс. руб. w
Сталь арматурная Прокат листовой

Решение. Уд. вес прод. наэкспорт ,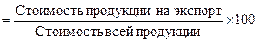

или – стоимость всей продукции. Воспользуемся формулой средней гармонической взвешенной. Средний удельный вес продукции на экспорт

Задача 4. Проведена малая выборка из партии электролампочек для определения продолжительности их службы. Определить значения моды и медианы.

№ лампочки	Срок горения, час.

Произведем ранжирование данных по возрастанию 1270; 1370; 1380; 1400; 1400; 1400; 1420; 1430; 1450. Мода Мо = 1400, так как это значение признака встречается три раза.

Место медианы . Me = 1400 – значение признака на 5-ом месте в ранжированном ряду.

Задача 5. Перевозка грузов по автотранспортному предприятию такова. Определить среднемесячный темп роста объема грузовых перевозок.

Месяц	Январь	Февраль	Март
Перевезено грузов, тыс. т	37,0	40,5	42,0

Решение. Определим цепные коэффициенты роста объема грузовых перевозок

.

Среднемесячный темп роста определим по формуле средней геометрической

Задача 6. Имеются следующие данные о товарообороте магазина. Определить среднюю цену мужского костюма.

Товары	Товарооборот, тыс. руб. w	Цена за единицу, руб. х
Костюм мужской, х/б Костюм мужской, п/ш Костюм мужской, ч/ш

Решение. Применим формулу расчета средней гармонической взвешенной