Множення многочлена на многочлен

Помножимо многочлен а + b на многочлен c + d. Щоб звести множення цих многочленів до множення многочлена на одночлен, позначимо много­член c + d через х. Тоді:

(a + b)(c + d) = (a + b) x = ax + bx.

Повернувшись до заміни х = c + d, матимемо:

ax + bx = a (c + d) + b (c + d) = ac + ad + bc + bd.

Отже, добутком многочлена а + b і многочлена c + d є многочлен ac + ad + bc + bd:

(a + b)(c + d) = ac + ad + bc + bd.

Вираз ac + ad + bc + bd ми одержали б одразу, якби помножили a на c і d, потім b на c і d і одержані добутки додали. Можна сказати й так: добуток ac + ad + bc + bd можна одержати, якщо помножити кожний член многочлена a + b на кожний член многочлена с + d й одержані добутки додати.

Приходимо до такого правила:

Щоб помножити многочлен на многочлен, досить кожний член одного многочлена помножити на кожний член іншого многочлена й одержані добутки додати.

Помножимо за цим правилом многочлен 2 а ² + b ² на многочлен 2 а - b:

(2 а ² + b ²)(2 а - b) = 2 a ² × 2 a + 2 a ² × (- b) + b ² × 2 a + b ² × (- b) =

= 4 a ³ - 2 a ² b + 2 ab ² - b ³.

Виконуючи множення многочленів, проміжні результати можна не записувати:

(2 а ² + b ²)(2 а - b) = 4 a ³ - 2 a ² b + 2 ab ² - b ³.

У наведених прикладах добуток двох многочленів ми записували у вигляді многочлена. Взагалі, добуток будь-яких многочленів завжди можна записати у вигляді многочлена.

Приклади розв’язання вправ

Приклад 1. Виконати множення:

а) (2 x ² - xy + 4 y ²)(2 x - 3 y); б) (a + b)(а + 1)(b - 1).

● а) (2 x ² - xy + 4 y ²)(2 x - 3 y) = =

= 4 x ³ - 8 x ² y + 11 xy ² - 12 y ³.

б) Знайдемо добуток перших двох многочленів, а потім одержаний добуток помножимо на третій многочлен:

(a + b)(а + 1)(b - 1) = (a ²+ а + bа + b)(b - 1) =

= a ² b - a ² + аb - a + b ² a - ba + b ² - b = a ² b - a ² - a + ab ²+ b ² - b. ●

Приклад 2. Розв’язати рівняння (х - 2)(2 х + 3) - х (2 х + 4) = 3.

● 2 х ² + 3 х - 4 х - 6- 2 х ² - 4 x = 3; -5 х - 6 = 3; -5 х = 9; х = -1,8.

Відповідь. -1,8. ●

Усно

422. Виконайте множення:

a) (a + 2)(b + 1); б) (a + b)(c - d); в) (x + y)(a + b - c).

Рівень А

Перемножте многочлени:

423. а) (x + 2)(y + z); б) (b + а)(c - 3);

в) (m - 4)(n + k); г) (a - b)(x - y);
д) (2 a - 3 b)(2 с + 5); е) (4 a + 6 b)(3 d - 2 c);

є) (x + y)(a - 5 b + 2); ж) (2 - c)(a - b - 2); з) (m - n + 1)(k + l).

424. а) (a + b)(c + 3); б) (2 x + y)(3 - 3 z); в) (a - 2 b)(3 х - 4 y);

г) (m + n)(a - b + 1); д) (a + b - 2)(с + 5); е) (2 x - y - 1)(a - 3 b).

Перетворіть вираз у многочлен стандартного вигляду:

425. a) (a + 3)(4 a - 3); б) (5 b - 4)(3 b - 2);

в) (a ² + 3 a - 4)(3 a - 2); г) (n - m)(n + 4 m);

д) (a - 6 b)(2 a - b); е) (4 c - 3 d)(3 c + d).

426. а) (а - 2)(а + 3); б) (3 x + 2)(2 x - 1);

в) (a + 5 b)(a - b); г) (4 x - 3 y)(x - 2 y).

Спростіть вираз:

427. а) (3 a - 4)(2 a + 1) + 5 a; б) (y + 3)(y - 4) - y (y - 1);

в) (2 x - 5)(2 x + 3) - 4(x ² - x); г) (a ² + a - 2)(а + 3) + 6 - 4 а ²;

д) (a + b)(a - 3 b) + 2 ab; е) (- х + 4 y)(2 x - y) + 2 x ² - 9 xy.

428. а) (x + 2)(2 x + 3) - 2 x ²; б) (a - 4)(3 a - 4) + 16 a - 16;

в) (a + 2 b)(3 а -4 b) + 3 аb - 3 а ²; г) -7 mn + (m + 5 n)(2 m - 3 n).

Розв’яжіть рівняння:

429. а) (х - 1)(х + 2) - x ² = 3; б) (2 y - 1)(2 - y) + 2 y ² = 1.

430. а) (х + 3)(х - 1) - х ² = 5; б) 5 х ² + (1- х)(5 х + 2) = 5.

Рівень Б

Перетворіть вираз у многочлен стандартного вигляду:

431. а) (-3 а + 2)(2 а ² + 2 a - 3); б) (3 x ²- 2 x + 1)(2 x ²+ 5 x);

в) (n ²- n + 3)(n ²+ 2 n + 2); г) (2 b ² - 3 b - 2)(4 b ²+ b - 4);

д) (c + 2)(c + 3)(c -5); е) (2 x + 1)(2 x -5)(x ² + 3 x + 2);

є) ж)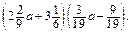

432. а) (4 а + 3)(а ² - 4 a + 2); б) (b ²- 2 b + 3)(3 b ²- 2 b + 1);

в) (x - 2)(x + 5)(x - 4); г) (2 y - 3)(y + 2)(4 y ²+ 3 y - 3);

д) 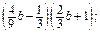е)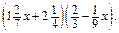

433. а) (а + b)(а ² + 5 ab - b ²); б) (4 x ²- 3 xy + y ²)(2 x - 7 y);

в) (3 n ²- 2 nm - m ²)(3 n - 2 m); г) (3 a - 2 b)(а - 2 b)(a ²+ 2 ab).

434. а) (2 x + y)(x ² + 2 xy - 2 y ²); б) (a - b)(а + 2 b)(3 a - 2 b).

Спростіть вираз:

435. а) (3 a - 1)(2 a + 5) + (2 a - 5)(3 a + 1);

б) (x + 7)(8 x - 1) - (2 x + 3)(4 x - 1);

в) (a - 2)(1 - 2 a + 2 a ²) - 2(a ³ - 3 a ² - 1);

г) (a ²- 2 ab + 4 b ²)(a + 2 b) - a ³ - b ³;

д) (3 xy ² - 7 x ² y)(3 xy ² - 2 x ² y) +(3 xy)³ - (3 xy ²)².

436. а) (4 x - 3)(3 x + 4) + (2 x - 3)(3 x + 1);

б) (2 b - 7)(4 b - 1) - (8 b - 3)(b + 1);

в) (x + 3 y)(x ²- 3 xy + 9 y ²) - 18 y ³;

г) (a + b)(a + b - 1) - a (a - 1) - b (b - 1).

Розв’яжіть рівняння:

437. а) (х - 1)(х - 3) = (х - 2)(х + 3);

б) (2 y - 1)(1 - y) + (y + 1)(2 y - 3) = 0;

в) (0,5 х - 3,5)(6 х + 2) + 30 х = 3 х (х - 3) - 26;

г)

438. а) (х + 6)(х - 4) = (х - 5)(х + 4);

б) (0,5 x + 7)(4 x - 1) - (x + 14)(2 x - 1) = 9;

в)

Доведіть, що значення виразу не залежать від значень х:

439. а) (х + 1)(х + 4) - (х + 2)(х + 3);

б) (1 - х)(2 - х)(3 - х) + (x - 4)(x ²- 2 x + 3).

440. (х - 3)(x ²+ 7 x - 3) - (х + 2)(x ²+ 2 x - 28).

Доведіть, що для кожного цілого значення k значення виразу:

441. (2 k + 1)(3 k + 2) - (2 k - 1)(3 k - 2) ділиться на 14.

442. (3 k + 2)(4 k - 3) - (2 k + 3)(k - 2) ділиться на 10.

443. Доведіть, що вираз (а ² + 3)(а ² - 1) - (а ² + 4)(а ² - 2) набуває лише додатних значень.

Доведіть тотожність:

444. а) (х + 3)(х ² - 1) = (х ² + 2 х - 3)(х + 1);

б) (a - b)(b - c)(c - a) = ab (b - a) + bc (c - b) + ca (a - c).

445. а) (а + 2)(а ² - 2 а - 3) = (а - 3)(а ² + 3 а + 2);

б) (a + b)(b - c) - (a - b)(b + c) = 2(b ²- ac).

446. Знайдіть три послідовних цілих числа, квадрат найменшого з яких на 11 менший від добутку двох інших чисел.

447. Довжина прямокутника в 1,8 разу більша від ширини. Якщо довжину прямокутника збільшити на 3 см, а ширину зменшити на 2 см, то площа зменшиться на 9 см². Знайдіть довжину і ширину прямокутника.

448.Довжина прямокутника на 4 см більша від ширини. Якщо довжину прямокутника зменшити на 1 см, а ширину збільшити на 2 см, то площа збільшиться на 10 см². Знайдіть довжину і ширину прямокутника.

Рівень В

449. Спростіть вираз (х - а)(х - b)(х - с)...(х - z), що є добутком 26 множників, у яких від змінної х віднімаються змінні, позначені всіма 26 буквами латинського алфавіту.

450. Спростіть вираз (n ¾ натуральне число):

а) (aⁿ + bⁿ)(aⁿ - bⁿ + 1) - a ^{2 n} + b ^{2 n} ; б) (1 + 2 ^{n + 1})(5- 2 ^{n + 1}) + 4 ^{n + 1}.

451. Доведіть тотожність:

а) (a + b + c)(a ² + b ² + c ² - ab - bc - ca) = a ³ + b ³ + c ³ - 3 abc;

б) a ³ + b ³ + c ³ = 3 abc, якщо a + b + c = 0.

452. а) Одне із цілих чисел при діленні на 6 дає в остачі 2, а друге ¾ в остачі 3. Доведіть, що добуток цих чисел ділиться на 6 без остачі.

б) Числа a, b і c при діленні на 4 дають відповідно в остачі 1, 2 і 3. Доведіть, що число abc + 2 ділиться на 4 без остачі.

453. Дано чотири послідовних цілих числа. Що більше — добуток найменшого і найбільшого із цих чисел чи добуток інших двох чисел — і на скільки більше?

454. Дві ділянки прямокутної форми мають рівні площі. Довжина другої ділянки на 2 м менша, ніж довжина першої, а ширина другої ділянки на 1 м більша, ніж ширина першої. Доведіть, що довжина першої ділянки удвічі більша від ширини другої.

455. Дано два многочлени:

х ⁴ + 987 х ³ – 876 х ² + 765 х – 654 і 9876 х ⁴ – 9800 х ² – 75.

Чому дорівнює сума коефіцієнтів многочлена стандартного вигляду, який є добутком даних многочленів?