Для рассмотрения устанавливающегося процесса нагрева тела от источников тепла, расположенных внутри тела

Пусть внутри тела действует источник тепла постоянной мощ­ности Р. Введем следующие предположения:

температура тела в любой момент времени одинакова во всех точках объема тела;

теплоемкость тела С не зависит от температуры;

коэффициент теплоотдачи практически не зависит от превыше­ния температуры и одинаков по всей поверхности тела.

За время dt энергия, генерируемая в теле, будет расходоваться на повышение температуры тела (Cdτ),а часть ее 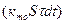будет отдаваться в окружающую среду:

. (6.30)

Следовательно, уравнение процесса нагрева тела

. (6.31)

Частное решение последнего уравнения

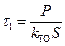. (6.32)

Общее решение дополнительного уравнения

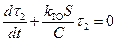, (6.33)

будет

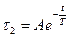, (6.34)

где А — постоянная интегрирования, определяемая условиями задач.

Величина равная отношению полной теплоемкости С тела к его теплоотдающей способности 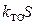называется постоянной времени.

Общее решение уравнения:

. (6.35)

Для определения постоянной А используем следующее условие: при

t=0 должно быть

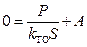т.е. . (6.36)

Подставляя полученное выражение, будем иметь

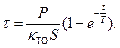(6.37)

На рис.6.6 представлено графическое изображение последнего выражения, из которого видно, что при t = ∞

(6.38)

Откуда следует, что

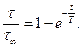(6.39)

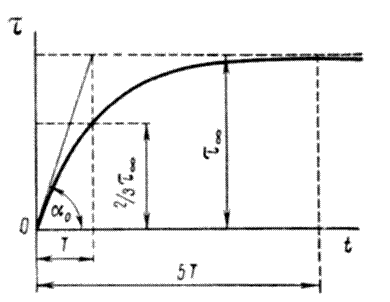
Рис.6.6. Зависимость превышения температуры от времени

при нагреве однородного тела

Таким образом, т₀ равно установившемуся превышению темпе­ратуры, когда выделяемая мощность Р становится численно равной мощности, отдаваемой в окружаю­щую среду с поверхности нагре­того тела.

Очевидно

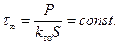(6.40)

Из (6.39)следует:

или 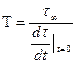. (6.41)

Касательная к кривой 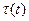в начале координат отсекает на пря­мой отрезок, равный в выбранном масштабе постоянной вре­мени Т.

Нетрудно показать, что при t=T

. (6.42)

На основании этого можно определять постоянную времени Т как время, необходимое для достижения 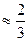установившегося превышения температуры (см. рис.6.6).

С точностью 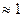% можно считать, что процесс установления температуры происходит через время, равное 5T.

После отключения аппарата начинается его охлаждение. Так как энергия, подводимая к аппарату, равна нулю, то левая часть также равна нулю:

. (6.43)

Решение уравнения (6.43) имеет вид:

(6.44)

где А — постоянная интегрирования, равная

(6.45)

Окончательно получаем: