Проверка адекватности модели

Проверка адекватности математической модели данным эксперимента проводится только в случае ненасыщенного планирования на основе сопоставления дисперсии воспроизводимости среднего значения функции отклика σ²(y) и дисперсии адекватности. Оценка дисперсии адекватности при N > m характеризует отклонения между результатами наблюдений и значениями, формируемыми по функции отклика

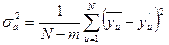, N>m,

где m – количество оцениваемых коэффициентов модели;

– среднее значение результатов наблюдения в u -й точке плана;

y^'_u – значение отклика в этой же точке, предсказанное на модели.

Количество степеней свободы дисперсии адекватности σ σ _a = N – m.

При насыщенном планировании нет степеней свободы и сумма отклонений равна нулю.

Проверка адекватности сводится к проверке гипотезы об однородности оценки дисперсии воспроизводимости σ² (y) с количеством степеней свободы σ (y) и оценки дисперсии адекватности. Проверка осуществляется по критерию Фишера аналогично рассмотренной выше проверке однородности дисперсий воспроизводимости. Оценки дисперсий в формуле расчета критерия расставляются так, чтобы его величина была больше единицы, критическая область является двусторонней.

F - критерий Фишера используют для сравнения дисперсий двух вариационных рядов. Он вычисляется по формуле:

,

где - большая дисперсия, - меньшая дисперсия.

Если вычисленное значение критерия F больше критического для определенного уровня значимости и соответствующих чисел степеней свободы для числителя и знаменателя, то дисперсии считаются различными.

Число степеней свободы числителя определяется по формуле:

,

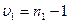где - число вариант для большей дисперсии.

Число степеней свободы знаменателя определяется по формуле:

,

где - число вариант для меньшей дисперсии.

В программе Excel проверка однородности дисперсий осуществляется с помощью функции ФТЕСТ (рис. 48). F-тест возвращает одностороннюю вероятность того, что дисперсии аргументов массив1 и массив2 различаются несущественно. Эта функция используется для того, чтобы определить, имеют ли две выборки различные дисперсии. Например, если даны результаты тестирования для частных и общественных школ, то можно определить, имеют ли эти школы различные уровни разнородности учащихся по результатам тестирования.

Рис. 48. Функция ФТЕСТ

ФТЕСТ (массив1; массив2)

Массив1— это первый массив или интервал данных.

Массив2— это второй массив или интервал данных.

Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.

Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются.

Если количество точек данных в аргументе массив1 или массив2 меньше 2, или если дисперсия аргумента массив1 или массив2 равна нулю, то функция ФТЕСТ возвращает значение ошибки #ДЕЛ/0!.

В надстройке «Пакет анализа» используется двухвыборочный F-тест для дисперсии.

Элементы диалогового окна «Двухвыборочный F-тест для дисперсии» приведены на рис. 49. Элементы диалогового окна «Двухвыборочный F-тест для дисперсии» совпадают с элементами диалогового окна «Двухвыборочный t-тест с одинаковыми дисперсиями».

Рис. 49. Двухвыборочный F-тест для дисперсии

Двухвыборочный F-тест применяется для сравнения дисперсий двух генеральных совокупностей.

Например, можно использовать F-тест по выборкам результатов заплыва для каждой из двух команд. Это средство предоставляет результаты сравнения нулевой гипотезы о том, что эти две выборки взяты из распределения с равными дисперсиями, с гипотезой, предполагающей, что дисперсии различны в базовом распределении.

С помощью этого средства вычисляется значение f F-статистики (или F-коэффициент). Значение f, близкое к 1, показывает, что дисперсии генеральной совокупности равны. В таблице результатов, если f < 1, "P(F <= f) одностороннее” дает возможность наблюдения значения F-статистики меньшего f при равных дисперсиях генеральной совокупности и F критическом одностороннем выдает критическое значение меньше 1 для выбранного уровня значимости Alpha. Если f > 1, “P(F <= f) одностороннее” дает возможность наблюдения значения F-статистики большего f при равных дисперсиях генеральной совокупности и F критическом одностороннем выдает критическое значение большее 1 для Alpha.

Значения критерия Фишера (F-критерия) для уровня значимости p = 0.05

f₁ - число степеней свободы большей дисперсии, f₂ - число степеней свободы меньшей дисперсии

	f1
f2
	161.45	199.50	215.71	224.58	230.16	233.99	236.77	238.88	240.54	241.88	245.95
	18.51	19.00	19.16	19.25	19.30	19.33	19.35	19.37	19.38	19.40	19.43
	10.13	9.55	9.28	9.12	9.01	8.94	8.89	8.85	8.81	8.79	8.70
	7.71	6.94	6.59	6.39	6.26	6.16	6.09	6.04	6.00	5.96	5.86
	6.61	5.79	5.41	5.19	5.05	4.95	4.88	4.82	4.77	4.74	4.62
	5.99	5.14	4.76	4.53	4.39	4.28	4.21	4.15	4.10	4.06	3.94
	5.59	4.74	4.35	4.12	3.97	3.87	3.79	3.73	3.68	3.64	3.51
	5.32	4.46	4.07	3.84	3.69	3.58	3.50	3.44	3.39	3.35	3.22
	5.12	4.26	3.86	3.63	3.48	3.37	3.29	3.23	3.18	3.14	3.01
	4.96	4.10	3.71	3.48	3.33	3.22	3.14	3.07	3.02	2.98	2.85
	4.84	3.98	3.59	3.36	3.20	3.09	3.01	2.95	2.90	2.85	2.72
	4.75	3.89	3.49	3.26	3.11	3.00	2.91	2.85	2.80	2.75	2.62
	4.67	3.81	3.41	3.18	3.03	2.92	2.83	2.77	2.71	2.67	2.53
	4.60	3.74	3.34	3.11	2.96	2.85	2.76	2.70	2.65	2.60	2.46
	4.54	3.68	3.29	3.06	2.90	2.79	2.71	2.64	2.59	2.54	2.40
	4.49	3.63	3.24	3.01	2.85	2.74	2.66	2.59	2.54	2.49	2.35
	4.45	3.59	3.20	2.96	2.81	2.70	2.61	2.55	2.49	2.45	2.31
	4.41	3.55	3.16	2.93	2.77	2.66	2.58	2.51	2.46	2.41	2.27
	4.38	3.52	3.13	2.90	2.74	2.63	2.54	2.48	2.42	2.38	2.23
	4.35	3.49	3.10	2.87	2.71	2.60	2.51	2.45	2.39	2.35	2.20

Если вычисленное значение критерия меньше критического, то нет оснований для сомнений в адекватности модели. Однако положительный исход статистической проверки не гарантирует достоверной адекватности, а тем более истинности модели (хотя и не противоречит такому предположению). Когда гипотеза отклоняется, следует вывод о неадекватности модели, следовательно, она заведомо не является истинной. Дальнейшее применение неадекватной модели обычно нецелесообразно, и надо принять меры по ее совершенствованию.

Причиной неадекватности могут являться: ошибки в организации и проведении опытов, например неконтролируемое изменение неучтенных в модели факторов; погрешности в задании исходных данных и в измерении результатов; большой размах варьирования факторов и другие причины. Иначе говоря, анализ причин неадекватности требует серьезного изучения сущности исследуемого процесса и методов его исследования.

Литература