Сравнение нескольких дисперсий нормальных генеральных совокупностей по выборкам различного объема. Критерий Бартлетта

Н₀: D(X₁)=D(X₂) =D(X₃)=… =D(X_l)

Введем обозначения

k_i=n_i-1 – число степеней свободы дисперсии S²_i/

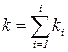- сумма чисел степеней свободы

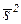– средняя арифметическая исправленных дисперсий

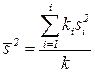
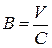– случайная величина (критерий Бартлетта).

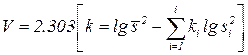
И по таблице критических точек распределения по уровню значимости и числу степеней свободы l-1 (l– число выборок). Найти критическую точку правосторонней критической области.

Если B<χ_кр² – нет оснований отвергнуть нулевую гипотезу

Если B> χ_кр²– отвергаем нулевую гипотезу

Критерий Бартлетта весьма чувствителен к отклонениям распределения от нормального, поэтому к выводам, полученным по этому критерию надо относиться осторожно.