 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Второго порядка 1 страница
|
|
Ортогональным планом называется такой план, у которого матрица планирования Х строится так, что бы матрица С=ХtХ оказалась диагональной. Используем этот подход и при построении планов второго порядка.
При ортогональных факторных планах каждый фактор варьируют симметрично относительно начала координат на двух уровнях. Этого достигают, принимая верхний уровень + 1, а нижний -1. При таком нормировании факторов обеспечиваются упрощения последующих вычислений. При этом число различных экспериментов N, определяемое числом всех неповторяющихся комбинаций, которые можно составить из k рассматриваемых независимых переменных, имеющих по два уровня, будет N - 2k. Таким образом, если осуществить все 2* возможных и неповторяющихся. Значимость коэффициентов проверяют по t-критерию Стьюдента, для чего сначала определяют статистический критерий, а затем значимость сравнивают с табличным значением tTa6jI, взятым из таблицы t-распределения Стьюдента по вероятности проверяемой гипотезы р и количеству степеней свободы, с которым определялось. Если для каждого коэффициента t > tTa6jI, то они все значимы. Затем определяют доверительные интервалы для каждого из коэффициентов по формуле
После интерпретации модели экспериментатор принимает решение о проведении дальнейших исследований. Для этого вначале устанавливают, в какой мере каждый из факторов влияет на параметр оптимизации У. Знак плюс при коэффициенте свидетельствует, что с увеличением значения фактора растет Y, при знаке минус - увеличение значения фактора приводит к уменьшению параметра оптимизации У.
Если линейная модель адекватна, а все коэффициенты незначимы (кроме 60) (чаще всего это происходит вследствие большой ошибки эксперимента или узких интервалов варьирования), то необходимо увеличить точность эксперимента, расширить интервалы варьирования. Если линейная модель неадекватна, это значит, что не удается аппроксимировать поверхность отклика плоскостью. В этом случае изменяют интервалы варьирования, выбирают другую точку в качестве нулевого уровня, либо используют нелинейную модель и весь цикл повторяют.
План называется центральным, если все точки расположены симметрично относительно центра плана. ОЦКП – центральный симметричный ортогональный композиционный план.
В ОЦКП входят: ядро - план ПФЭ с N0 = 2n точками плана, n0 (одна для этого плана) центральная точка плана  и по две “звездные” точки для каждого фактора
и по две “звездные” точки для каждого фактора
 ,
,  ,
, 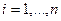 ,
,  ,
,  .
.
 – плечо “звездных” точек.
– плечо “звездных” точек.
При этом в каждой плоскости, содержащей ось Y и координатную ось i -того фактора (проходящей через центр плана), оказываются три значения фактора хi  и три соответствующих значения Y.
и три соответствующих значения Y.
Общее количество точек в плане ОЦКП составляет
 ,
,
где для ОЦКП n0 =1.
При n > 2 в ОЦКП оказывается меньшее количество точек, чем в плане ПФЭ 3n.
Число точек в плане
| n | |||||
| ОЦКП | |||||
ПФЭ 
|
Графическое представление ОЦКП для n =3 приведено на рис. 36.

Рис. 36. ОЦКП при n =3
Для ортогонального плана необходимо, чтобы выполнялось соотношение
 .
.
Так как  , то для столбцов j =1, 2,…., m +1 должно выполняться условие
, то для столбцов j =1, 2,…., m +1 должно выполняться условие
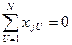 .
.
Это означает необходимость выполнения требования, чтобы сумма элементов любого столбца (кроме j =0), включая столбцы, соответствующие квадратам фактора, должна быть равна нулю. Это возможно, если члены столбцов, соответствующих квадратам факторов, преобразованы, иначе сумма квадратов факторов не может быть равна нулю.
Преобразование элементов этих столбцов осуществляется в виде
 ,
,
где а – величина, зависящая от числа факторов.
Сумма элементов столбца, соответствующего квадратам факторов
 .
.
Откуда
 .
.
В общем случае ортогональный центрально-композиционный план при трех (n) факторов имеет следующий вид
| U | x0 | x1 | x2 | x3 | x1x2 | x1x3 | x2x3 | x1x2x3 | x4= x12-a | x5= x22-a | x6= x32-a | Y | |
| Точки плана ПФЭ 23 (N0=2n точек) | +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | 1 – a | 1 – a | 1 – a | Y1 | |
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | 1 – a | 1 – a | 1 – a | Y2 | ||
| +1 | -1 | +1 | -1 | -1 | +1 | -1 | -1 | 1 – a | 1 – a | 1 – a | Y3 | ||
| +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | 1 – a | 1 – a | 1 – a | Y4 | ||
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | 1 – a | 1 – a | 1 – a | Y5 | ||
| +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 | 1 – a | 1 – a | 1 – a | Y6 | ||
| +1 | -1 | +1 | +1 | -1 | -1 | +1 | +1 | 1 – a | 1 – a | 1 – a | Y7 | ||
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | -1 | 1 – a | 1 – a | 1 – a | Y8 | ||
| Звездные точки 2n точек | +1 | -α | α2 – a | -a | -a | Y9 | |||||||
| +1 | + α | α2 – a | -a | -a | Y10 | ||||||||
| +1 | -α | -a | α2 – a | -a | Y11 | ||||||||
| +1 | + α | -a | α2 – a | -a | Y12 | ||||||||
| +1 | -α | -a | -a | α2 – a | Y13 | ||||||||
| +1 | + α | -a | -a | α2 – a | Y14 | ||||||||
| Нулевая точка | +1 | -a | -a | -a | Y15 | ||||||||

| - | N | |||||||||||

| - | N | 2n+2a2 | 2n | 2n(1-a)2+2(a2-a)2+ +a2(2n-2) +n0a2 |
В ОЦКП каждый фактор фиксируется, в общем случае, на пяти уровнях (-  , -1, 0, 1, +
, -1, 0, 1, +  ).
).
Для определения неизвестных “а” и “  ” нужно сформировать и решить систему из двух уравнений. Одно из них для “а” мы записали раннее. Другое уравнение получим из условия ортогональности для столбцов
” нужно сформировать и решить систему из двух уравнений. Одно из них для “а” мы записали раннее. Другое уравнение получим из условия ортогональности для столбцов  и
и 
 .
.
После простейших преобразований с учетом того, что  – общее число опытов в плане, получаем соотношение
– общее число опытов в плане, получаем соотношение
 .
.
Соотношение для а при j =1, 2 или 3 может быть записано как (см. план)
 .
.
Подставив его в последнее уравнение получаем
 ,
,
откуда константа преобразования а

 .
.
Тогда

и плечо звездных точек
 .
.
Например, для ОЦКП при числе факторов n =3 имеем следующие параметры плана
 ,
,  ,
,
 ;
;  ,
,
 ,
,  ,
,  .
.
Сам план принимает вид
| U | x0 | x1 | x2 | x3 | x1x2 | x1x3 | x2x3 | x1x2x3 | x4= x12-a | x5= x22-a | x6= x32-a | Y | |
| Точки плана ПФЭ 23 (N0=2n точек) | +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | 0,27 | 0,27 | 0,27 | Y1 | |
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | 0,27 | 0,27 | 0,27 | Y2 | ||
| +1 | -1 | +1 | -1 | -1 | +1 | -1 | -1 | 0,27 | 0,27 | 0,27 | Y3 | ||
| +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | 0,27 | 0,27 | 0,27 | Y4 | ||
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | 0,27 | 0,27 | 0,27 | Y5 | ||
| +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 | 0,27 | 0,27 | 0,27 | Y6 | ||
| +1 | -1 | +1 | +1 | -1 | -1 | +1 | +1 | 0,27 | 0,27 | 0,27 | Y7 | ||
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | -1 | 0,27 | 0,27 | 0,27 | Y8 | ||
| Звездные точки 2n точек | +1 | -1,215 | 0,75 | -0,73 | -0,73 | Y9 | |||||||
| +1 | + 1,215 | 0,75 | -0,73 | -0,73 | Y10 | ||||||||
| +1 | -1,215 | -0,73 | 0,75 | -0,73 | Y11 | ||||||||
| +1 | + 1,215 | -0,73 | 0,75 | -0,73 | Y12 | ||||||||
| +1 | -1,215 | -0,73 | -0,73 | 0,75 | Y13 | ||||||||
| +1 | + 1,215 | -0,73 | -0,73 | 0,75 | Y14 | ||||||||
| Нулевая точка | +1 | -0,73 | -0,73 | -0,73 | Y15 | ||||||||

| - | N | |||||||||||

| - | N | 2n+2a2 | 2n | 2n(1-a)2+2(a2-a)2+ +a2(2n-2) +n0a2 |
Очевидно, что план является ортогональным. В отличие от планов ПФЭ для ОЦКП сумма квадратов факторов разных столбцов не является одинаковой.
По результатам опытов плана формируется полином
 .
.
Коэффициенты полинома  определяется как
определяется как
 .
.
Можно преобразовать полином к виду
 ,
,
где
 .
.
Значения параметров ОЦКП при числе факторов n
| n | |||||||
| α | 1,125 | 1,414 | 1,596 | 1,761 | 1,909 | 2,045 | |
| a | 0,667 | 0,73 | 0,8 | 0,86 | 0,91 | 0,946 | 0,968 |
| N |
При n =2 ОЦКП совпадает с планом ПФЭ 23. Звездные точки ОЦКП в этом случае лежат на границах варьирования факторов. Если точки плана ПФЭ 2n всегда лежат на окружности (поверхности шара, гипершара), то точки плана ОЦКП не лежат на какой-либо одной окружности (поверхности шара, гипершара). План ОЦКП не является насыщенным. Так, например, для n = 3 полином имеет одиннадцать членов со своими коэффициентами, но для их определения используются пятнадцать опытов.
Планы второго порядка с единичной областью планирования
Так как ОЦКП и РОЦКП - композиционные планы, то при естественной области планирования “звездные” точки могут выходить за пределы единичного гиперкуба и единичного гипершара. Для вписывания плана в область единичного гипершара необходимо изменить значение факторов путем умножения их на коэффициент
 .
.
Так при  n=2,
n=2,
 .
.
Значение факторов в ОЦКП и РОЦКП при переходе от естественной области планирования к единичному гипершару, при n = 2.
| U | ОЦКП | РЦКП | ||

| 
| 
| 
| |
| -0,707 | -0,707 | -0,707 | -0,707 | |
| +0,707 | -0,707 | +0,707 | -0,707 | |
| -0,707 | +0,707 | -0,707 | +0,707 | |
| +0,707 | +0,707 | +0,707 | +0,707 | |
| -0,707 | -1 | |||
| +0,707 | +1 | |||
| -0,707 | -1 | |||
| +0,707 | +1 | |||
| - | ||||
| - | ||||
| - | ||||
| - | ||||
| - | ||||
| - | ||||
| - |
Могут использоваться рототабельные планы с точками плана в вершинах других, кроме квадрата (куба, суперкуба), правильных многогранников, вписанных в область единичного круга (шара, гипершара). В рототабельном плане на основе N 0-угольника присутствуют N 0 отличающихся точек на окружности, с радиусом R 1=1, и n 0 совпадающих точек в центре плана, с радиусом R 2=0. При n =2 для квадратичного полинома при шести его членах число отличающихся точек плана должно быть не менее шести. В планах на основе пятиугольника (шестиугольника или семиугольника) присутствуют 6 (7 или 8) отличающихся точек, что меньше чем в ОЦКП и РОЦКП, у которых 9 отличающихся точек. При соответствующем выборе многоугольника можно сформировать насыщенный рототабельный план второго порядка. Значения факторов в точках плана определяются типом многоугольника.
Рототабельные планы
Рототабельные планы – это планы, у которых точки плана располагаются на окружностях (сферах, гиперсферах). У рототабельного плана первого порядка точки плана располагаются на одной окружности (сфере, гиперсфере) с радиусом R
 ,
,
где V =1,…, N - номер точки плана, i =1,…, n – номер фактора.
В таком случае точность оценивания функции отклика по любому направлению факторного пространства (для всех точек плана) одинаковая.
Рототабельный план может быть симметричным, когда точки плана располагаются симметрично друг друга. Рассмотренный ранее план ПФЭ 2n – рототабельный симметричный план первого порядка.
У рототабельных планов второго порядка точки плана располагаются на двух концентрических гиперсферах с радиусами R 1 и R 2. В таких планах
 ,
,
для V =1,…, N 0 и
 ,
,
для W =1,…, n 0,
где V и W – текущие номера точек плана в двух подмножествах опытов N 0 и n 0 из их общего количества N, относящихся к двум разным концентрическим сферам. Одна из сфер может быть вырожденной, когда R 2=0. Рассмотренный ранее ортогональный центрально-композиционный план второго порядка (ОЦКП) не является рототабельным планом, так как его точки лежат на трех концентрических окружностях (сферах, гиперсферах). При n =2 это очевидно из рис. 37. “Звездные” точки плана и точки плана ПФЭ 2n лежат на разных окружностях.

Рис. 37. Расположение точек ОЦКП на трех окружностях
Рототабельный план может быть ортогональным, если выполняется условие
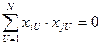 ,
,
где i=1,…,m, j=1,…,n, m>n, i≠j - номера столбцов плана.
Рототабельный ортогональный центрально-композиционный план
Рототабельный ортогональный центрально-композиционный план (РОЦКП) строится аналогично рассмотренному ранее ОЦКП. К использованному в качестве ядра плану ПФЭ 2n добавляются “звездные” точки - по две на каждый фактор и несколько точек в центре плана. “Звездные” точки должны располагаться на поверхности гиперсферы с радиусом R, на которой лежат и точки плана ПФЭ 2n, то есть величина плеча “звездных” точек 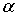 должна равняться радиусу R. Это может быть обеспечено, при выполнении условия ортогональности, только при соответствующем выборе числа наблюдений в центральной (нулевой) точке плана n 0. Для РОЦКП n 0 зависит от числа факторов n. В ОЦКП n 0 = 1 для любого числа n.
должна равняться радиусу R. Это может быть обеспечено, при выполнении условия ортогональности, только при соответствующем выборе числа наблюдений в центральной (нулевой) точке плана n 0. Для РОЦКП n 0 зависит от числа факторов n. В ОЦКП n 0 = 1 для любого числа n.
Радиус сферы, на которой лежат точки плана ПФЭ 2n при двух уровнях варьирования факторов с диапазоном  1 составляет (рис. 38)
1 составляет (рис. 38)

Рис. 38. Радиус окружности (сферы), на которой лежат точки плана ПФЭ 2n при диапазоне варьирования факторов от –1 до +1:
а) - n =1,  ;
;
б) - n =2,  ;
;
в) - n =3, 
 .
.
Таким образом, при построении РОЦКП с ядром из плана ПФЭ 2n плечо “звездных” точек определяется числом факторов
 .
.
Раннее при определении параметров ортогонального композиционного плана второго порядка с ядром из плана ПФЭ 2n было получено
 ,
,
где  - число точек плана ПФЭ,
- число точек плана ПФЭ,
 - полное число точек композиционного плана второго порядка,
- полное число точек композиционного плана второго порядка,
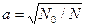 - константа преобразования элементов столбцов, соответствующих квадратам факторов.
- константа преобразования элементов столбцов, соответствующих квадратам факторов.
В этом случае для РОЦКП число наблюдений в центре плана
 .
.
Если n 0 не целое, то при практическом построении плана его округляют до целого, но свойство ортогональности плана нарушается.
Параметры РОЦКП в зависимости от числа факторов
| n | ||||||||

| 1,414 | 1,732 | 2,236 | 2,45 | 2,646 | 2,83 | ||

| 10,5 | 13,13 | 14,25 | 15,53 | ||||

| ||||||||
| N | 24,5 | 55,13 | 157,55 | |||||
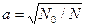
| 0,5 | 0,5 | 0,574 | 0,67 | 0,76 | 0,84 | 0,9 | 0,94 |
Дата публикования: 2014-11-04; Прочитано: 2062 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
