Полный факторный эксперимент

Эффективное решение научных и прикладных задач исследований различных процессов и явлений предполагает учет, по возможности, всей совокупности факторов и их взаимных связей, оказывающих влияние на параметры оптимизации. Поэтому в настоящее время для описания сложных объектов и явлений применяют, как правило, методы многофакторного планирования эксперимента, т.е. многофакторный анализ (факторный анализ).

Полный факторный эксперимент – эксперимент, реализующий все возможные неповторяющиеся комбинации уровней исследуемых факторов. В результате ПФЭ получают не сечения статических характеристик объекта, как это имеет место в классическом однофакторном методе, а функциональную зависимость выходного параметра от всех воздействующих на него факторов 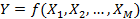, что очень существенно.

Факторный анализ широко применяется в настоящее время как в естественных (технических и экономических), так и в гуманитарных науках. Основные его положения были разработаны английским психологом Эдуардом Спирменом.

Факторный анализ может быть качественным и количественным. На стадии качественного анализа отбираются наиболее важные факторы, качественно связанные с изучаемым вопросом, значения которых можно определить. На стадии количественного анализа с использованием специальных математических критериев отбираются факторы, влияние которых на исследуемый процесс или явление существенно. В многофакторных моделях существенными (значительными) обычно оказываются те факторы, которые с результативным признаком имеют значимую связь, а между собой – несущественную.

Пусть интересующее нас свойство (Y) объекта зависит от нескольких (М) независимых переменных 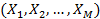и необходимо выяснить характер этой зависимости - 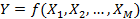. Величина Y называется «отклик», а сама зависимость 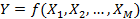- «функция отклика».

Отклик должен быть определен количественно. Однако могут встречаться и качественные признаки Y. В этом случае возможно применение рангового подхода. Пример рангового подхода – оценка на экзамене, когда одним числом оценивается сложный комплекс полученных сведений о знаниях студента.

Диапазоны изменения факторов X задают область определения Y. Если принять, что каждому фактору соответствует координатная ось, то полученное пространство называется факторным пространством. Если число факторов М=2, область определения Y представляет собой прямоугольник, при М=3 – куб, при М 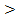3 – гиперкуб. Геометрическое представление функции отклика в факторном пространстве 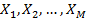называется поверхностью отклика.

Если исследуется влияние на Y лишь одного фактора 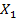, то определение функции отклика – достаточно простая задача. Задавшись несколькими значениями этого фактора, в результате опытов получают соответствующие значения Y и график .

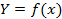Если факторов два, то необходимо провести опыты при разных соотношениях этих факторов. Полученную функцию отклика в трехмерном пространстве можно анализировать, проводя ряд сечений с фиксированными значениями одного из фактров. Вычлененные графики сечений можно аппроксимировать совокупностью математических выражений.

Если цель эксперимента состоит в оценке наиболее простым способом функции отклика, то в такой постановке эксперимент называют интерполяционным, т.е. основанным на интерполяции – нахождении функции по некоторым ее значениям.

Более сложным является экстремальный эксперимент, предназначенный для определения оптимума. Критерий оптимальности формулируется исследователем. В математическом смысле целью экстремальных экспериментов является поиск экстремума функции отклика.

Планирование и проведение ПФЭ обладает рядом существенных преимуществ по сравнению с традиционными методами экспериментальных работ:

· Резко сокращается число испытаний;

· Вся схема исследования оказывается значительно формализованной. Исследования распадаются на логически связанные этапы;

· План эксперимента определяет четкую стратегию (последовательность действий), позволяющую принимать обоснованные решения после каждой серии опытов;

· Процедура разработки математических моделей значительно упрощается;

· Точность математических моделей (их адекватность результатам эксперимента) повышается;

· Разработанные математические модели позволяют глубже выявить механизм явления и определить оптимальные значения сразу всех факторов 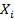(так как они действуют на реальный процесс и изменяются одновременно), при которых значения всех функций оптимизации 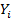также оптимальны.