Графоаналитический метод

Кинематическое исследование механизмов графическим методом наряду со своей простотой и наглядностью имеет ряд недостатков (неточность вычислений, потребность дополнительных вычислений и др.). Более точным методом кинематического исследования механизмов является графоаналитический способ, основанный на построении планов скоростей и ускорений.

Планом скоростей (ускорений) называют рисунок, на котором в заранее выбранном масштабном коэффициенте изображены векторы, равные по модулю и направле­нию скоростям (ускорениям) различных точек звеньев механизма в данный момент времени. План скоростей (ускорений), построен­ный для исследуемого положения механизма, - это - совокупность нескольких планов скоростей (ускорений) отдельных точек звень­ев, у которых полюса планов являются общей точкой - полюсом плана скоростей (ускорений) механизма.

Планы скоростей (ускорений) механизма могут как строиться для каждого положения отдельно, так и быть совмещенными.

Рассмотрим построение планов скоростей и ускорений начального звена.

Если начальное звено механизма совершает вращательное дви­жение, то скорость его любой точки, например В (рис. 2.8, а), будет равна:

,

где l_АВ - кратчайшее расстояние от оси вращения до точки В; ω₁ - угловая скорость звена АВ. Скорость точ­ки В перпендикулярна прямой АВ (V_B ^ АВ) и может быть изображена на плане скоростей (рис. 2.8, б) вектором , модуль которого будет 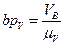, где - масштабный коэффициент скорости, 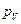- полюс плана скоростей, - одноименная точка на звене. Аналогичным образом могут быть найдены и построены ско­рости любых других точек, принадлежащих этому звену.

Рис. 2.8. Скорости, ускорения точки В и ее планы

На рис. 2.8, в построен план ускорений для этой же точки В на­чального звена АВ. На плане ускорений изображен вектор уско­рения точки В - ā_В и составляющие: нормальное и каса­тельное ускорения. Соответствующие векторы на плане уско­рений построены по следующим соотношениям:

- нормальное ускорение :

; ; ,

где - полюс плана ускорений, - масштабный коэф­фициент плана ускорений;

- касательное ускорение :

; ; ,

где - угловое ускорение звена;

- ускорение :

; .

Ускорения других точек начального звена находятся и строятся аналогичным образом.

Рассмотрим построение планов скоростей и ускорений при сложном движении звена (рис. 2.9).

При сложном движении объекта его кинематические харак­теристики определяются проще, если движение исследуется одновременно в неподвижной (основной) и подвижной системах отсчета.

Движение объекта относительно основной системы отсчета на­зывается абсолютным движением.

Движение объекта относительно подвижной системы отсчета называется относительным движением.

Движение подвижной системы отсчета относительно основной называется переносным движением.

Элементы абсолютного движения обозначаются индексом а, относительного - r, переносного - е. Эти индексы используют тогда, когда в обозначении не указывают точку, движение которой рассматривается.

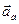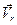При сложном движении тела абсолютная(ое) скорость (уско­рение ) точки равна векторной сумме переносной(го) () и относительной(го) () скоростей (ускорений) этой точки, т. е.

; (2.13)

, (2.14)

где и - соответственно нормальное ускорение в относи­тельном движении, направленное по нормали.

Если рассматривается совокупность взаимосвя­занных объектов, то вместо этих индексов вводят обозначение точки и номер звена, которому она принадлежит, например , . Если принадлежность точек к звену оговорена отдельно или ясно видна по структурной схеме, то номер звена можно опускать, например , .

Соотношения (2.13) и (2.14) используют для построения планов скоростей и ускорений точек звеньев. Векторные уравнения (2.13 и (2.14), например для точек В и С звена ВС (рис. 2.9), примут вид соответственно:

;

; или .

Рис. 2.9. Планы скоростей и ускорений звена ВС

Из последних выражений следует, что абсолютная(ое) скорость (ускорение ) точки С равна векторной сумме переносной(го) скорости (ускорения 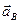), определяемой движением точки В, и относительной(го) скорости (ускорения ) точ­ки С при вращении звена вокруг точки В. Если известны траекто­рии αα и ββ, описываемые точками С и В в абсолютном движении (рис. 2.9, а), то направление всех скоростей и ускорений определе­но. Значит, для решения последних уравнений необходимо знать модули скорости (ускорения) одной из точек, например В. При анализе векторных уравнений принято подчеркивать известные векторы одной или двумя чертами внизу, под которыми также мо­гут указываться и их направления. Две черты обозначают, что век­тор известен как по величине, так и по направлению. Одна черта означает, что для вектора известно либо направление, либо величина.

Графические решения представленных уравнений показаны на рис. 2.9, в в виде отрезков, изображающих в масштабе соответст­вующие величины.

Скорость любой точки S, расположенной на звене ВС, находит­ся в соответствии со свойствами планов скоростей и ускорений, путем пропорционального деления отрезка cb..

Рассмотрим принципы построения планов скоростей и ускорений на примере механизмов 2 класса, состоящих из структурных групп 1, 2 и 3 видов, как наиболее часто встречающихся.

Будем считать, что размеры всех звеньев и расположение точек на звеньях из­вестны, и известен закон движения входного звена 1 (угловая скорость ω₁ и угловое ускорение ε₁ определены).

На рис. 2.10, а изображена схема кривошипно-коромыслового механизма, со­стоящего из стойки 0, входного звена 1, звеньев 2 и 3, образующих структур­ную группу 2 класса 1 вида. На звене 2 расположена точка К, на звене 3 — точка М.

Скорость точки В определяется выражением. Вектор направлен перпендикулярно звену АВ в сторону вращения.

Движение точки С может быть разложено на переносно-поступательное со скоростью точки В или точки D и относительно-вращательное соответственно вокруг точки В или точки D. Векторные уравнения для скорости точки С будут иметь следующий вид:

В этих уравнениях известны по величине и направлению векторы и и (). Векторы же скоростей и известны только по направлению. Вектор скорости точки С относительно точки В направлен перпен­дикулярно звену ВС, вектор скорости точки С относительно точки D -перпендикулярно CD.

Рис. 2.10. Кривошипно-коромысловый механизм:

а – кинематическая схема; б – план скоростей; в – план ускорений

Величины векторов и определяются при построении плана ско­ростей (рис. 2.10, б). Скорость точки В изображается на плане отрезком pb, скорость — отрезком bс, скорость — отрезком рс. Т.к. , то абсолютная скорость точки С равна относительной скорости

.

Величины скоростей точек будут определяться следующими выражения­ми:

Пользуясь планом скоростей, можно определить угловые скорости и звеньев 2 и 3.

Величины этих скоростей определяются из равенств

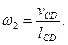
Направления угловых скоростей и могут быть определены следую­щим образом. Мысленно прикладывая векторы и к точке С, видим, что вращение звеньев 2 и 3 происходит в направлении вращения часо­вой стрелки (см. рис. 2.10, а).

Для определения скорости точки К, лежащей на звене ВС имеем векторное уравнение

Очевидно, что направление вектора совпадает с направлением вектора , т.е. отрезок плана скоростей (bк), определяющий скорость , совпада­ет по направлению с отрезком (bc).

Разделив почленно равенства, получаем:

или

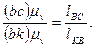
откуда

Из последнего выражения следует: чтобы определить отрезок плана скоро­стей, изображающий относительную скорость , необходимо отрезок (bс), изображающий на плане скоростей относительную скорость разделить в том же отношении, в котором точка К делит звено 2.

Из плана скоростей находим

.

Рассуждая аналогичным образом, определяем на плане скоростей отрезок (рт), изображающий вектор скорости точки М, лежащей на звене 3. Скорость точки М будет равна

.

При построении плана ускорений, как и при построении плана скоростей, рассматриваем движение точки С как сложное, состоящее из переносного по­ступательного с ускорением точек В и D и относительного вращательного вокруг этих точек.

Векторные уравнения для определения ускорения с точки С будут сле­дующими:

В этих уравнениях

,

,

;

,

где , , – нормальные ускорения;

, , – тангенциальные ускорения.

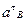При известных величинах угловой скорости ω₁, и углового ускорения ε₁, звена 1 и определяются выражениями:

; .

Нормальные ускорения и также могут быть определены:

; .

Вектор ускорения направлен от точки В к точке А, вектор ускорения от точки С к точке В, вектор ускорения – от точки С к точке D. Вектор тангенциального ускорения направлен перпендикулярно звену АВ в сторону ε₁. Векторы и известны только по направлению. Вектор направлен перпендикулярно звену ВС, а вектор – перпендикулярно звену DC.

Величины векторов и определяются из построения плана уско­рений. Развернутые векторные уравнения для определения вектора уско­рения точки С, которые и определяют последовательность построения плана имеют вид:

План ускорений показан на рис. 2.10, в. Из плана ускорений находим ускорения точек:

,

,

,

.

Значение условных ускорений ε ₂ и ε ₂ звеньев 2 и 3 будут равны

; .

Направления угловых ускорений ε ₂ и ε ₂ могут быть определены сле­дующим образом. Перенося мысленно векторы и в точку С. видим, что направление ε ₂ и ε ₂ противоположно направлению вращения часовой стрелки (см. рис. 2.10, а).

Для определения ускорения точки К воспользуемся уравнением

.

Направление вектора должно совпадать на плане ускорений с направ­лением вектора , так как для всех точек звена величины угловой скорости ω ₂ и углового ускорения ε ₂ одинаковы. Величина отрезка (bk), изображающего на плане ускорений ускорение , определяется из условия пропорциональ­ности ускорений радиусам-векторам, т.е.

,

или

,

откуда

.

Из этого выражения следует: чтобы определить отрезок плана ускорений, изображающий ускорение , необходимо отрезок (bс) плана, изображаю­щий ускорение , разделить в том же отношении, в каком точка К делит звено 2. Найдя положение точки К на плане и соединив ее с полюсом π, получим отрезок (πk), изображающий полное ускорение точки К. Величина ускорения равна

.

Рассуждая подобным образом, определяем положение точки m на плане ускорений и строим отрезок (πm), изображающий ускорение точки М, лежащей на звене 3 (см. рис. 2.10, в). Величина ускорения будет равна

.

На рис. 2.11, а показана схема кривошипно-ползунного механизма, состояще­го из стойки ОX, входного звена, а также звеньев 2 и 3, образующих структурную группу 2 класса 2 вида.

Не останавливаясь на подробном описании построения планов скоростей и ускорений, приведем векторные уравнения для определения векторов скоро­сти и ускорения точки В, а также необходимые формулы для нахож­дения составляющих этих уравнений, вычисления искомых скоростей и уско­рений точек, угловых скоростей и ускорений звеньев.

где , .

Рис.2.11. Кривошипно-ползунный механизм:

а - кинематическая схема; б - план скоростей; в - план ускорений

План скоростей изображен на рис. 2.11, б. Из плана скоростей находим

; .

Угловая скорость ω₂ звена 2 будет равна

.

Векторные уравнения для определения ускорения точки В следующие (принимаем, что ε₁=0):

где , , , - кориолисово ускорение (, так как ).

План ускорений представлен на рис. 2.11, в. Из плана ускорений находим:

; .

Угловое ускорение ε₂ звена 2

.

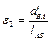На рис. 2.12, а показана схема кулисного механизма, состоящего из стойки, входного звена 1, а также звеньев 2 и 3, образующих структурную группу 2 класса 3 вида.

Рассматривая движение звеньев кулисного механизма, необходимо иметь в виду, что звено 2 соединяет подвижные звенья 1 и 3, т.е. имеет место поступательное движение точки А₃, принадлежащей звену 3 и точки А₁ принадлежащей звену 1.

Векторные уравнения, определяющие скорость точки А₃ будут иметь следующий вид:

где - вектор скорости движения точки А₃ относительно А₁ (направлен вдоль звена 3); - вектор скорости переносного движения точки А₃ относительно В (направление перпендикулярно звену 3).

Величина скорости точки С определяется из следующего соотношения:

,

т.е.

,

или

где и - отрезки на плане скоростей (см. рис.2.12, б).

Рис.2.12. Кулисный механизм:

а - кинематическая схема; б – план скоростей; в – план ускорений.

Из плана скоростей находим:

;

;

;

.

Для определения вектора ускорения точки A ₃ составим векторные уравнения (принимаем, что ε₁=0):

где , , , .

Направление вектора кориолисова ускорения определяется вектором скорости ,повернутым на 90⁰ по направлению угловой скорости ω₃.

Ускорение точки С определяется из соотношения:

,

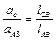Откуда или ,

где и - отрезки на плане ускорений (рис.2.12, в).

Из плана ускорений находим:

, ;

;

;

.

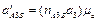Таким образом, с помощью планов скоростей и ускорений можно определить кинематические характеристики движения любой точки или звена механизма.