 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пересечение двух многогранников
|
|
Для построения линии пересечения многогранных поверхностей определяют точки, в которых ребра одной из поверхностей пересекают грани другой и ребра второй пересекают грани первой (задача на пересечение прямой линии с плоскостью). Через найденные точки в определенной последовательности проводят ломаную линию.
В том случае, когда один из многогранников занимает частное положение (т.е. его боковые грани проецируются на одну из плоскостей проекций в многоугольник), задача построения линии их пересечения решается достаточно просто. Проекция линии пересечения совпадает с проекцией многогранника на той плоскости проекций, где он – многоугольник. Задача сводится к построению отсутствующих проекций ломаной линии.
Частное положение может занимать только призма.
Пример 7.1. Построить проекции линии пересечения пирамиды и призмы частного положения (рис. 7.1).
1. Призма расположена так, что все ее боковые грани перпендикулярны П1. На П1 ее боковая поверхность проецируется в линию, точнее в треугольник D1E1F1. И горизонтальной проекцией линии пересечения призмы DEFD*E*F* и пирамиды SABC является ломаная линия 11Е151.
2. Грани призмы пересекают также грани SBC и SAB пирамиды. Отметим точки излома линии пересечения 11Е151, расположенные на пересечении ее с ребрами пирамиды. А именно точки 11, 21, 31, 41, 51, 61. Т.к. ребро ЕЕ* призмы пересекает две грани SAB и SAC пирамиды, то 31 ≡61.
|
|
Пример 7.2. Построить проекции линии пересечения поверхностей общего положения: четырехугольной пирамиды SABCD и треугольной призмы TFGE*F*G* (рис. 7.2).
|
1. Через ребра призмы EE', FF', GG' проводим вспомогательные плоскости уровня Ф, Ф', Ф''. Горизонтальные проекции линий пересечения этих плоскостей с призмой совпадают с проекциями ребер призмы.
|
Там, где эта линия пересекает ребро G2G2', лежит фронтальная проекция 72 точки пересечения ребра GG' и грани SAD пирамиды. По линиям связи находим горизонтальную проекцию точки - 71.
3. Применяя вспомогательную плоскость Ф', аналогично строим точку 52, а по ней находим горизонтальную проекцию - 51.
4.Применяя вспомогательную плоскость Ф'', аналогично строим точку 42, а по ней находим горизонтальную проекцию точки – 41.
5. Горизонтальная проекция линии пересечения плоскости Ф''' и граней EGG'E' и FGG'F' призмы проходит вдоль А1С1, через точки 91 и 101 на основании призмы. По линиям связи находим положение точек 92 и 102, через которые проводим образующие призмы, параллельные ее боковым ребрам. На пересечении с ребрами S2A2 получим точки 62 и 82. Затем по линиям связи определяем горизонтальные проекции этих точек – 61 и 81.
6. Соединив одноименные проекции точек, получаем фронтальную 425262728242 и горизонтальную 415161718141 проекции замкнутой ломаной линии пересечения призмы и пирамиды.
7. Определяем видимость отдельных участков линии пересечения и ребер многогранников.
Задача 7.1.Построить проекции пирамиды со сквозным призматическим отверстием.

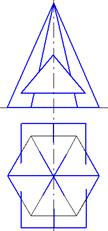
| Задача 7.2.Построить проекции линии пересечения пирамиды с призмой.
| |
Задача 7.3.Построить проекции линии пересечения пирамиды с призмой.

| Задача 7.4.Построить проекции линии пересечения призмы с пирамидой.

|
Дата публикования: 2014-11-03; Прочитано: 5518 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!


