Пример 1. Представить в тригонометрической форме комплексные числа: , , ,

Представить в тригонометрической форме комплексные числа: , , , .

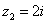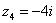На самом деле задание устное. Для наглядности перепишу тригонометрическую форму комплексного числа:

Запомним намертво, модуль – длина (которая всегда неотрицательна), аргумент – угол.

1) Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что . Формальный расчет по формуле: .
Очевидно, что (число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме: .

Ясно, как день, обратное проверочное действие:

2) Представим в тригонометрической форме число 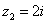. Найдем его модуль и аргумент. Очевидно, что 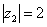. Формальный расчет по формуле: .
Очевидно, что (или 90 градусов). На чертеже угол обозначен красным цветом. Таким образом, число в тригонометрической форме: .

Используя таблицу значений тригонометрических функций, легко обратно получить алгебраическую форму числа (заодно выполнив проверку):

3) Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что . Формальный расчет по формуле: .
Очевидно, что (или 180 градусов). На чертеже угол обозначен синим цветом. Таким образом, число в тригонометрической форме: .

Проверка:

4) И четвёртый интересный случай. Представим в тригонометрической форме число 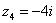. Найдем его модуль и аргумент. Очевидно, что . Формальный расчет по формуле: .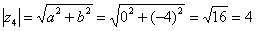

Аргумент можно записать двумя способами: Первый способ: (270 градусов), и, соответственно: . Проверка:

18.2 ДЕЙСТВИЯ С КОМПЛЕКСНЫМИ ЧИСЛАМИ В ТРИГОНОМЕТРИЧЕСКОЙ ФОРМЕ