 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пример 2. Тогда, по формуле Муавра:
|
|
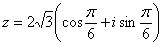 найти
найти 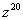 .
.
Тогда, по формуле Муавра:
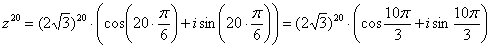
Упаси боже, не нужно считать на калькуляторе 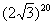 , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляет
, а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляет 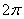 радиан или 360 градусов. Смотрим сколько у нас оборотов в аргументе
радиан или 360 градусов. Смотрим сколько у нас оборотов в аргументе 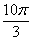 :
: 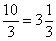 оборотов, в данном случае можно убавить один оборот:
оборотов, в данном случае можно убавить один оборот: 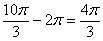 . Надеюсь всем понятно, что
. Надеюсь всем понятно, что 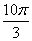 и
и 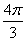 – это один и тот же угол.
– это один и тот же угол.
Таким образом, окончательный ответ запишется так:
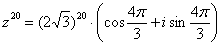
Любители стандартов везде и во всём могут переписать ответ в виде:
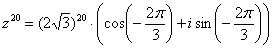 (т.е. убавить еще один оборот и получить значение аргумента в стандартном виде).
(т.е. убавить еще один оборот и получить значение аргумента в стандартном виде).
Хотя 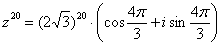 – ни в коем случае не ошибка.
– ни в коем случае не ошибка.
ПРАКТИКУМ 18
ЗАДАНИЕ N 1
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа 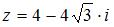 имеет вид …
имеет вид …
Решение:
Для представления комплексного числа в тригонометрической форме записи
необходимо найти его модуль и аргумент.
Используя формулу 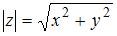 , где
, где 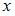 – действительная, а
– действительная, а 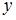 – мнимая часть комплексного числа, получим:
– мнимая часть комплексного числа, получим:
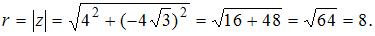
По формулам 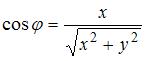 и
и 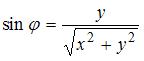 найдем аргумент
найдем аргумент 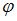 комплексного числа.
комплексного числа.
Обращаем внимание, что под аргументом 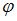 понимается его главное значение, то есть значение, удовлетворяющее условию
понимается его главное значение, то есть значение, удовлетворяющее условию 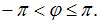
Так как 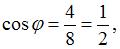
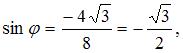 то
то 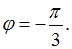
Зная, что тригонометрическая форма комплексного числа имеет вид
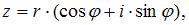 получим:
получим: 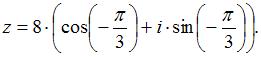
ЗАДАНИЕ N 2
Тема: Тригонометрическая форма комплексного числа
Произведение комплексных чисел 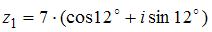 и
и 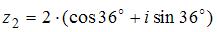 равно …
равно …
Решение:
Воспользуемся формулой: 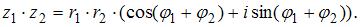 Получим:
Получим: 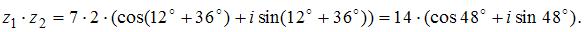
ЗАДАНИЕ N 3
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа 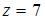 имеет вид …
имеет вид …
Решение:
Для представления комплексного числа в тригонометрической форме записи необходимо найти его модуль и аргумент.
Заметим, что мнимая часть данного комплексного числа равна нулю, поэтому 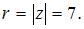
Точка, изображающая это число, принадлежит положительной части действительной оси, значит, 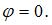
Зная, что тригонометрическая форма комплексного числа имеет вид
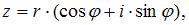 получим:
получим: 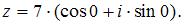
ЗАДАНИЕ N 4
Тема: Тригонометрическая форма комплексного числа
Частное 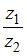 комплексных чисел
комплексных чисел 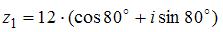 и
и 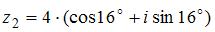 равно …
равно …
Решение:
Воспользуемся формулой: 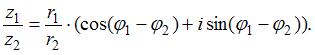 Получим:
Получим:
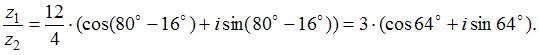
ЗАДАНИЕ N 5
Тема: Тригонометрическая форма комплексного числа
Степень комплексного числа 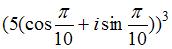 равна …
равна …
Решение:
Согласно формуле Муавра 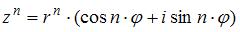 находим:
находим:
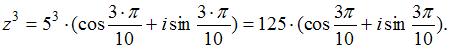
САМОСТОЯТЕЛЬНАЯ РАБОТА 18
ЗАДАНИЕ N 1
Тема: Тригонометрическая форма комплексного числа
Степень комплексного числа 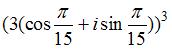 равна …
равна …
ЗАДАНИЕ N 2
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа 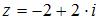 имеет вид …
имеет вид …
ЗАДАНИЕ N 3
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа 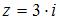 имеет вид …
имеет вид …
ЗАДАНИЕ N 4
Тема: Тригонометрическая форма комплексного числа
Частное 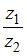 комплексных чисел
комплексных чисел 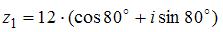 и
и 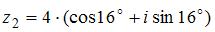 равно …
равно …
ЗАДАНИЕ N 5
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа 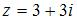 имеет вид …
имеет вид …
ЗАДАНИЕ N 6
Тема: Тригонометрическая форма комплексного числа
Частное 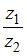 комплексных чисел
комплексных чисел 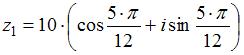 и
и 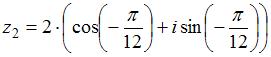 равно …
равно …
ЗАДАНИЕ N 7
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа 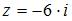 имеет вид …
имеет вид …
ЗАДАНИЕ N 8
Тема: Тригонометрическая форма комплексного числа
Степень комплексного числа 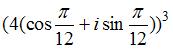 равна …
равна …
ЗАДАНИЕ N 9
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа 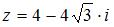 имеет вид …
имеет вид …
ЗАДАНИЕ N 10
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа 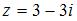 имеет вид …
имеет вид …
ЗАДАНИЕ N 11
Тема: Тригонометрическая форма комплексного числа
Частное 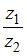 комплексных чисел
комплексных чисел 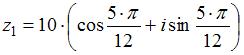 и
и 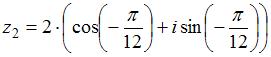 равно …
равно …
ЗАДАНИЕ N 12
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа 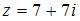 имеет вид …
имеет вид …
ЗАДАНИЕ N 13
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа 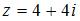 имеет вид …
имеет вид …
ЗАДАНИЕ N 14
Тема: Тригонометрическая форма комплексного числа
Произведение комплексных чисел 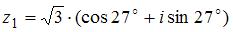 и
и 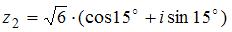 равно …
равно …
Дата публикования: 2014-11-03; Прочитано: 662 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
