Тригонометрическая форма комплексного числа

Любое комплексное число (кроме нуля) можно записать в тригонометрической форме:
, где – это модуль комплексного числа, а 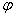– аргумент комплексного числа. Изобразим на комплексной плоскости число . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что :

Напоминаю, модулем комплексного числа 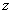называется расстояние от начала координат до соответствующей точки комплексной плоскости.

Модуль комплексного числа 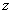стандартно обозначают: или

По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: . Данная формула справедлива для любых значений «а» и «бэ».

Аргументом комплексного числа 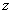называется угол 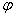между положительной полуосью действительной оси 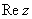и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: .

Аргумент комплексного числа 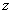стандартно обозначают: 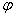или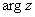

Из геометрических соображений получается следующая формула для нахождения аргумента:
. Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой. Эти случаи мы тоже разберем.

Но сначала рассмотрим простейшие примеры, когда комплексные числа располагаются на координатных осях.