 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пример 2. Найти неопределенный интеграл
|
|
Найти неопределенный интеграл.
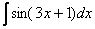
Идея метода замены состоит в том, чтобы сложное выражение (или некоторую функцию) заменить одной буквой.
В данном случае напрашивается: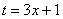 
Вторая по популярности буква для замены – это буква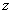 
.
В принципе, можно использовать и другие буквы, но мы всё-таки будем придерживаться традиций.
Итак: 
Но при замене у нас остаётся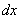 
! Наверное, многие догадались, что если осуществляется переход к новой переменной 
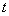, то в новом интеграле всё должно быть выражено через букву 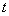, и дифференциалу 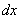там совсем не место.
Следует логичный вывод, что 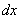нужно превратить в некоторое выражение, которое зависит только от.
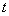Действие следующее. После того, как мы подобрали замену, в данном примере, 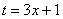, нам нужно найти дифференциал 
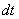. Так как 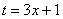, то
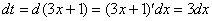
После разборок с дифференциалом окончательный результат рекомендую переписать максимально коротко: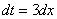 
Теперь по правилам пропорции выражаем нужный нам :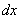
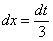
В итоге: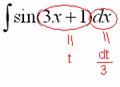 
Таким образом:
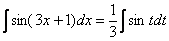
А это уже самый что ни на есть табличный интеграл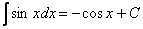 
(таблица, интегралов, естественно, справедлива и для переменной ).
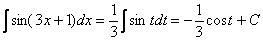
В заключении осталось провести обратную замену. Вспоминаем, что .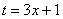
Готово.
11.3 ТАБЛИЦА ИНТЕГРАЛОВ
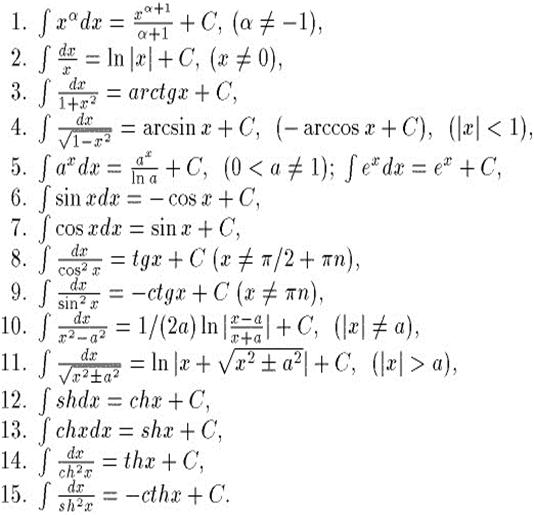
ПРАКТИКУМ 11
ЗАДАНИЕ N 1
Тема: Неопределенный интеграл
Неопределенный интеграл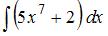 
равен …
Решение:
Напоминаем, что интеграл суммы двух функций равен сумме интегралов этих функций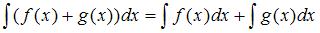 
и постоянный множитель можно выносить за знак неопределенного интеграла: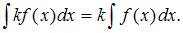 
Тогда, используя формулу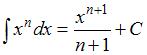 
, получим:
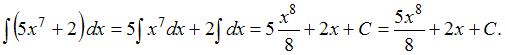
ЗАДАНИЕ N 2
Тема: Методы вычисления неопределенных интегралов
…
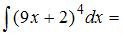Решение:
Подстановка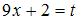 
приводит рассматриваемый интеграл к табличному: 
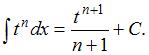Найдем дифференциал от обеих частей подстановки: 
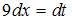, тогда 
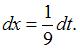Подставим получившиеся выражения в исходный интеграл:
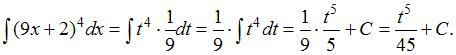Заменив 
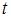его выражением из подстановки, получим: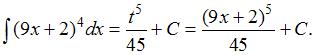 
ЗАДАНИЕ N 3
Тема: Неопределенный интеграл
…
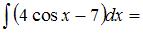Решение:
Напоминаем, что интеграл разности двух функций равен разности интегралов этих функций 
и постоянный множитель можно выносить за знак неопределенного интеграла: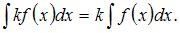 
Тогда, используя формулу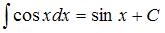 
, получим:
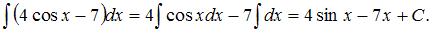
ЗАДАНИЕ N 4
Тема: Методы вычисления неопределенных интегралов
…
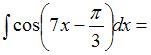Решение:
Подстановка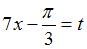 
приводит рассматриваемый интеграл к табличному: 
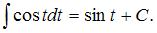Найдем дифференциал от обеих частей подстановки: 
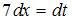, тогда 
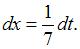Подставим получившиеся выражения в исходный интеграл: 
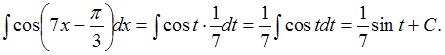Заменив 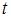его выражением из подстановки, получим: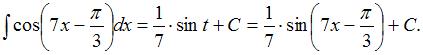 
ЗАДАНИЕ N 5
Тема: Неопределенный интеграл
Неопределенный интеграл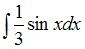 
равен …
Решение:
Напоминаем, что постоянный множитель можно выносить за знак неопределенного интеграла: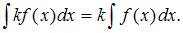
Тогда, используя формулу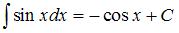 
, получим:
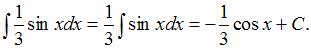
ЗАДАНИЕ N 6
Тема: Методы вычисления неопределенных интегралов
…
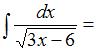Решение:
Подстановка 
приводит рассматриваемый интеграл к табличному: 
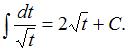Найдем дифференциал от обеих частей подстановки: 
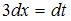, тогда 
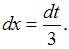Подставим получившиеся выражения в исходный интеграл:
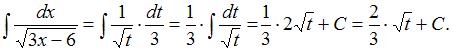Заменив 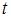его выражением из подстановки, получим: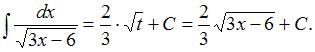 
ЗАДАНИЕ N 7
Тема: Методы вычисления неопределенных интегралов
…
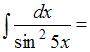Решение:
Подстановка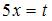 
приводит рассматриваемый интеграл к табличному: 
Найдем дифференциал от обеих частей подстановки: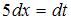 
, тогда 
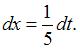Подставим получившиеся выражения в исходный интеграл: 
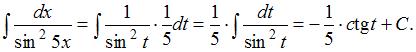Заменив 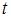его выражением из подстановки, получим: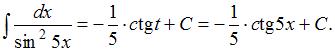 
ЗАДАНИЕ N 8
Тема: Неопределенный интеграл
…
Решение:
Напоминаем, что интеграл суммы двух функций равен сумме интегралов этих функций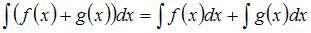 
и постоянный множитель можно выносить за знак неопределенного интеграла: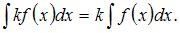
Тогда, используя формулу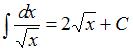 
, получим:
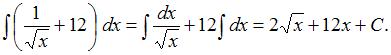
ЗАДАНИЕ N 9
Тема: Методы вычисления неопределенных интегралов
Неопределенный интеграл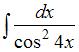 
равен …
Решение:
Обращаем внимание, что подстановка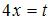 
приводит рассматриваемый интеграл к табличному: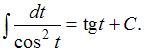 
Найдем дифференциал от обеих частей подстановки: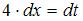 
, тогда
Подставим получившиеся выражения в исходный интеграл:
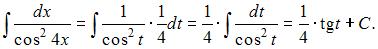
Заменив 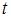его выражением из подстановки, получим:
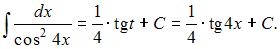
ЗАДАНИЕ N 10
Тема: Методы вычисления неопределенных интегралов
…
Решение:
Подстановка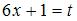 
приводит рассматриваемый интеграл к табличному: 
Найдем дифференциал от обеих частей подстановки: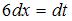 
, тогда 
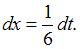Подставим получившиеся выражения в исходный интеграл:
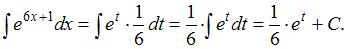Заменив 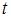его выражением из подстановки, получим: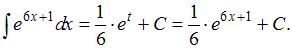 
САМОСТОЯТЕЛЬНАЯ РАБОТА 11
ЗАДАНИЕ N 1
Тема: Неопределенный интеграл
…
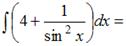ЗАДАНИЕ N 2
Тема: Неопределенный интеграл
…
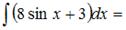ЗАДАНИЕ N 3
Тема: Методы вычисления неопределенных интегралов
…
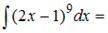ЗАДАНИЕ N 4
Тема: Неопределенный интеграл
…
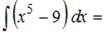ЗАДАНИЕ N 5
Тема: Методы вычисления неопределенных интегралов
Неопределенный интеграл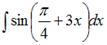 
равен …
ЗАДАНИЕ N 6
Тема: Неопределенный интеграл
…
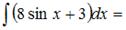ЗАДАНИЕ N 7
Тема: Методы вычисления неопределенных интегралов
…
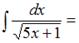ЗАДАНИЕ N 8
Тема: Неопределенный интеграл
Неопределенный интеграл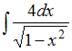 
равен …
ЗАДАНИЕ N 9 Тема: Неопределенный интеграл
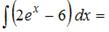
ЗАДАНИЕ N 10 Тема: Неопределенный интеграл
…
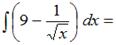Дата публикования: 2014-11-03; Прочитано: 443 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
