ЗАДАНИЕ N 2

Тема: Правила дифференцирования
Производная функции 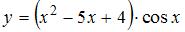равна …

Решение:
Для нахождения производной необходимо воспользоваться правилами
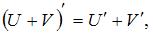
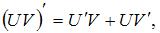
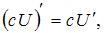где c – постоянная величина, а U и V – некоторые функции, зависящие от x, и формулами

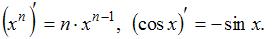
Тогда получим

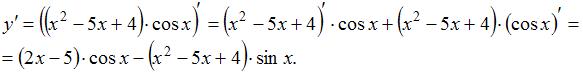
ЗАДАНИЕ N 3
Тема: Правила дифференцирования
Производная функции 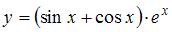равна …

Решение:
Для нахождения производной необходимо воспользоваться правилами
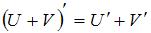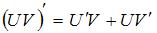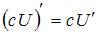, , , где c – постоянная величина, а U и V – некоторые функции, зависящие от x, и формулами

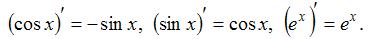
Тогда получим

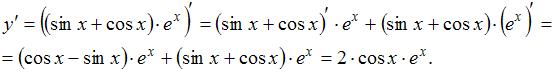
ЗАДАНИЕ N 4
Тема: Правила дифференцирования
Производная функции 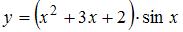равна …

Решение:
Для нахождения производной необходимо воспользоваться правилами
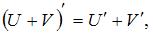
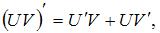
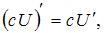где c – постоянная величина, а U и V – некоторые функции, зависящие от x, и формулами

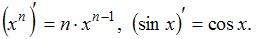
Тогда получим

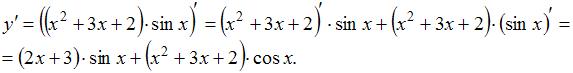
ЗАДАНИЕ N 5
Тема: Производная функции в точке
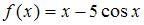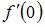Если , то принимает значение, равное …

Решение:
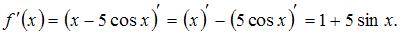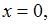Производная суммы двух функций равна сумме производных этих функций, значит, Пусть тогда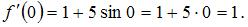

ЗАДАНИЕ N 6
Тема: Производная функции в точке
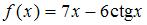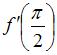Если , то принимает значение, равное …

Решение:
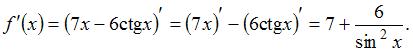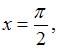Производная суммы двух функций равна сумме производных этих функций, значит, Пусть тогда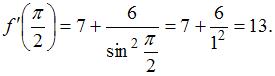

ЗАДАНИЕ N 8
Тема: Производная функции в точке
Если 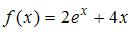, то 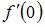принимает значение, равное …

Решение:
Напоминаем, что производная суммы двух функций равна сумме производных этих функций. Тогда имеем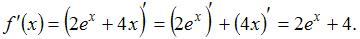
Пусть 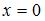. Получим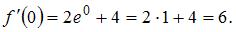

ЗАДАНИЕ N 9
Тема: Производная функции в точке
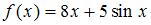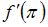Если , то принимает значение, равное …

Решение:
Производная суммы двух функций равна сумме производных этих функций, значит, 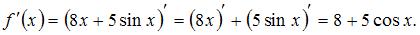Пусть тогда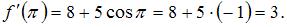

ЗАДАНИЕ N 10
Тема: Производная функции в точке
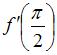Если , то принимает значение, равное …

Решение:
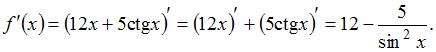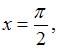Производная суммы двух функций равна сумме производных этих функций, значит, Пусть тогда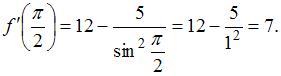

ЗАДАНИЕ N 11
Тема: Производная функции в точке
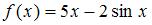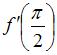Если , то принимает значение, равное …

Решение:
Производная суммы двух функций равна сумме производных этих функций, значит, 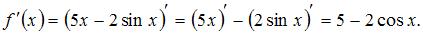Пусть , тогда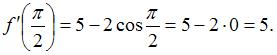

ЗАДАНИЕ N 12
Тема: Производная сложной функции
Производная функции 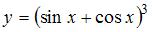равна …

Решение:
Данная функция является сложной.
Пусть 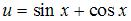, тогда 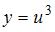. Напоминаем, что производная сложной функции находится по формуле 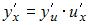. Тогда получим

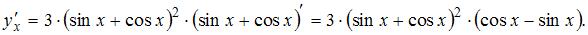
ЗАДАНИЕ N 13
Тема: Производная сложной функции
Производная функции 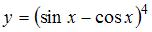равна …

Решение:
Данная функция является сложной. Пусть 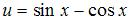, тогда 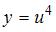. Напоминаем, что производная сложной функции находится по формуле 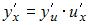. Тогда получим

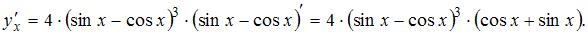
ЗАДАНИЕ N 14
Тема: Производная сложной функции
Производная функции 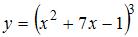равна …

Решение:
Данная функция является сложной.
Пусть 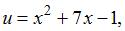тогда 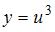. Напоминаем, что производная сложной функции находится по формуле 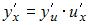. Тогда получим

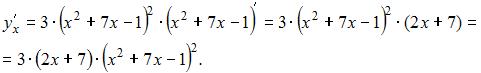
САМОСТОЯТЕЛЬНАЯ РАБОТА 8

ЗАДАНИЕ N 1
Тема: Правила дифференцирования
Производная функции 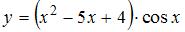равна …