Примеры решения задач. Решение: В отсутствии затухания суммарная энергия электрического и магнитного полей в контуре сохраняется

Задача 1. В колебательном контуре с индуктивностью и емкостью конденсатор заряжен до максимального напряжения . Каким будет ток в контуре в тот момент, когда напряжение на конденсаторе уменьшится в два раза? Колебания считать незатухающими.

Решение: В отсутствии затухания суммарная энергия электрического и магнитного полей в контуре сохраняется. Следовательно, в каждый момент времени справедливо равенство:

откуда

По условию задачи 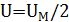. Ток в контуре в этот момент времени равен: .

Задача 2. В колебательном контуре конденсатору с емкостью сообщили заряд , после чего возникли затухающие электромагнитные колебания. Сколько тепла выделится к моменту, когда максимальное напряжение на конденсаторе станет меньше максимального напряжения в раза?

Решение: Количество выделившегося тепла равно разности между начальными и конечными значениями энергии в контуре. В моменты, когда напряжение на конденсаторе максимально, ток через катушку равен нулю. Следовательно, энергия в эти моменты сосредоточена в конденсаторе. Имеем:

Учитывая, что и в интересующий нас момент времени получаем ответ:

.

Задача 3. Катушка индуктивностью с сопротивлением обмотки и конденсатора емкостью подключены параллельно к источнику ЭДС и внутренним сопротивлением . Какое количество тепла выделится в контуре после отключения источника?

r

C

L

R

Рисунок 4.12 – К задаче 3

Решение: При замкнутом достаточно долгое время ключе в цепи устанавливается ток через источник и катушку, величина которого равна:

Напряжение на конденсаторе, равное напряжению на катушке, будет:

Суммарная энергия заряженного конденсатора и катушки с током:

После отключения источника в контуре, состоящем из катушки и конденсатора, возникнут затухающие электромагнитные колебания, в результате которых вся начальная энергия перейдет в тепло:

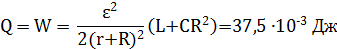
Задача 4. Конденсатор емкостью , заряженный до напряжения 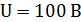, подсоединяют катушку индуктивности . Чему равна величина тока через катушку спустя время после подключения конденсатора? Сопротивлением катушки и соединительных проводов пренебречь.

Решение: При подключении заряженного конденсатора к катушке в образовавшемся контуре возникают электрические колебания с частотой 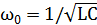. При этом заряд на конденсаторе меняется во времени по закону:

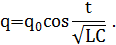
где - начальный заряд на конденсаторе. Поскольку сопротивление катушки и соединительных проводов пренебрежимо мало, суммарная энергия электрического и магнитного поля в контуре сохраняется. Из закона сохранения энергии следует, что:

Выражая отсюда ток через катушку, имеем:

Величина тока в момент времени равна:

Задача 5. Колебательный контур состоит из катушки индуктивности и четырех конденсаторов, соединенных как показано на рисунке. Во сколько раз изменится период собственных колебаний в контуре, если замкнуть ключ, соединяющий точки А и ?

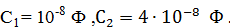
L

C

C

C

C

A

B

Рисунок 4.13 – К задаче 5

Решение: Поскольку период электромагнитных колебаний в контуре определяется формулой Томпсона отношение периода колебаний после замыкания ключа к периоду колебаний до замыкания ключа выразится как:

где - емкости батареи конденсаторов в этих двух случаях соответственно. Расчет по стандартным формулам дает:

при разомкнутом ключе,

при замкнутом ключе.

Отсюда получаем ответ:

Задача 6. В цепи, показанной на рисунке, конденсатор емкостью вначале заряжен до напряжения а конденсатор емкостью разряжен. До какого максимального значения может зарядиться конденсатор 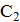в процессе колебаний, возникающих в цепи после замыкания ключа? Потерями в соединительных проводах и в катушке индуктивности пренебречь.

K

L

C

C

U

Рисунок 4.14 – К задаче 6

Решение: После замыкания ключа в цепи возникают гармонические колебания, в процессе которых происходит периодическая перезарядка конденсаторов. В каждый момент времени суммарное напряжение на конденсаторах равно напряжению на катушке, которое, в свою очередь, опережает по фазе ток в цепи на . В момент достижения максимального напряжения на конденсаторах ток в цепи обратится в нуль, следовательно, вся энергия будет сосредоточена на конденсаторах. При этом на конденсатор 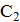перетечет из конденсатора некоторый заряд , а на конденсаторе останется заряд . Величину заряда на конденсаторе 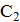можно найти из закона сохранения энергии в контуре. В силу того, что в рассматриваемый момент времени магнитная энергия обращается в нуль,

Отсюда . Учитывая, что , получаем ответ:

.

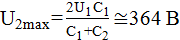Вывод: При решении задач следует уделять внимание как общим закономерностям, присущим колебательным процессам, так и физической сущности явлений, происходящих в электрическом колебательном контуре.

Контрольные вопросы второго уровня (сборник задач)

1. Напряжение, при котором зажигается или гаснет неоновая лампа, включенная в сеть переменного тока, соответствует действующему значению напряжения этой сети. В течение каждого полупериода лампа горит 2/3 мс. Найдите частоту переменного тока. [375 Гц]

2. К генератору переменного тока подключена электропечь, сопротивление которой 200 Ом. За 5 мин работы печи в ней выделяется 270 кДж теплоты. Какова при этом амплитуда силы тока, проходящего через печь? [3 А]

3. Во сколько раз уменьшится индуктивное сопротивление катушки, если ее включить в цепь переменного тока с частотой 50 Гц вместо 10 кГц? [В 200 раз]

4. Сопротивление 200 Ом и конденсатор подключены параллельно к источнику переменного тока с циклической частотой 2500 рад/с. Найдите емкость конденсатора, если амплитудное значение силы тока через сопротивление 1 А, а через конденсатор 2 А. [4 мкФ]

5. При какой циклической частоте переменного тока наступит резонанс напряжений в замкнутой цепи, состоящей из катушки с индуктивностью 0,5 Гн и конденсатора 200 мкФ? [0,1 рад/с]

6. Два соленоида с плотной намоткой имеют одинаковую длину и площадь круглого поперечного сечения. Соленоид 1 намотан вдвое более тонким проводом, чем соленоид 2. Чему равно отношение их индуктивностей? Чему равно отношение их постоянных времени (если в цепи нет других сопротивлений)? [В 2 раза]

7. Катушка обладает сопротивлением R= 1000 Ом и индуктивностью L = 0,300 Гн. Определите силу тока в катушке, если к ней приложено напряжение: а) 120 В постоянного тока; б) 120 В (эффективное значение) переменного тока с частотой 60 Гц. [а) 0,12 А; б) 0,119 А]

8. Постройте график зависимости импеданса конденсатора емкостью 1,6 мкФ от частоты в пределах от 10 до 1000 Гц.

9. Постройте график зависимости импеданса катушки с индуктивностью 2,0 мГн от частоты в пределах от 100 до 10 000 Гц.

10. Чему равен импеданс конденсатора емкостью 0,025 мкФ с хорошей изоляцией, который подключен к источнику напряжения 2,1 кВ (эффективное значение) с частотой 200 Гц? Чему равно пиковое значение силы тока? [32 кОм; 93 мА]

11. В последовательной LR-цепочке (R=160 Ом, L=0,85 мГн) течет ток I= 3,1 cos (377t) (где ток I измеряется в А, время t - в секундах). Какая мощность в среднем рассеивается в контуре? [769 Вт]

12. Колебательный контур состоит из конденсатора емкостью С = 2∙10^-8 Ф и катушки с общим числом витков N = 300 индуктивностью L = 5∙10^-5 Гн. Омическим сопротивлением контура пренебречь. Максимальное напряжение на обкладках конденсатора U₀ = 120 В. Определить максимальный магнитный поток, пронизывающий катушку, и начальную фазу колебаний напряжения, если в момент t = 0 энергия электрического поля конденсатора равна энергии магнитного поля катушки. [4∙10^-7 Вб; π/4]

13. Ток силой 70 А от сети 120 В при частоте 60 Гц, протекающий через тело человека в течение 1 с, может оказаться смертельным. Каким должен быть импеданс человеческого тела, чтобы сила тока достигла этой величины? [1,7 Ом]

14. Чему равно эффективное значение силы тока в RС-цепочке (R = 4,7 кОм, С=0,20 мкФ), включенной в сеть 120 В, с частотой 60 Гц? Чему равен сдвиг фаз между напряжением и током? Какая мощность рассеивается в цепочке? Чему равны эффективные значения падения напряжения на Rи С? [I_эфф = 8,68 мА; ϕ = -70°7'; N= 0,35 Вт; U_Rэфф = 40,8 В; U_Cэфф = = 112,8 В]

15. Чему равно эффективное значение силы тока в последовательной LR-цепочке (R = 65 Ом, L = 50,0 мГн), включенной в сеть 120 В, с частотой 60 Гц? Чему равен сдвиг фаз между напряжением и током? Какая мощность рассеивается в цепочке? Чему равны эффективные значения падения напряжения на R и L? [I_зфф= 1,77 мА; ϕ = -16°15'; N=204 Вт; U_Rэфф= 115 В; U_Lэфф = 33,3 В]

16. К RCL-цепочке (L= 1,2 Гн, R= 2,0 кОм, С=0,30 мкФ) приложено напряжение U= 8,1sin(754t) (U измеряется в В, t— в секундах). Определите импеданс и сдвиг фаз. Какая мощность рассеивается в цепочке? Чему равны эффективные значения силы тока и напряжения на каждом элементе цепи? [Z= 4 кОм; ϕ = -60°22'; N = 4,08 мВт; I_эфф=1,43 мА; U_Rэфф = 2,86 В; U_Lэфф = = 1,29 В; U_Сэфф = 6,29 В]

17. Электрическая цепь содержит два элемента. Причем неизвестно, что это - резистор, конденсатор или катушка индуктивности. Когда цепь подключают к источнику 120 В, 60 Гц, сила тока в ней составляет 8,1 А и опережает по фазе напряжение на 13°. Какие элементы входят в цепь и каковы их номиналы? [R= 14,3 Ом; С =700 мкФ]

18. Колебательный контур состоит из катушки индуктивностью L = 5 мГн и конденсатора емкостью С = 0,2 мкФ. При каком логарифмическом декременте и омическом сопротивлении цепи энергия уменьшится на порядок за три полных колебания? Какова относительная погрешность при расчете частоты по формуле собственных гармонических колебаний для найденного омического сопротивления? [0,38; 19 Ом; 4,2%]

19. Колебательный контур состоит из катушки (индуктивность L = 0,06 мГн, омическое сопротивление R = 2 Ом) и конденсатора (емкость С = 0,04 мкФ). Какую среднюю мощность должен потреблять контур, чтобы в нем поддерживались незатухающие колебания с амплитудными значениями напряжения на конденсаторе U₀ = 1,5 В? [1,5 Вт]

20. Катушка с индуктивностью 35 мГн и активным сопротивлением 2,0 Ом соединена последовательно с конденсатором 20 мкФ и источником напряжения 45 В, 60 Гц. Определите эффективное значение силы тока, сдвиг фаз и мощность, рассеиваемую в этой цепи. [I_эфф = 0,38 А; ϕ = 89°; N = 0,29 Вт]

21. Катушка с индуктивностью 23 мГн и сопротивлением 0,80 Ом подключена к конденсатору С и источнику напряжения с частотой 360 Гц. Какую емкость должен иметь конденсатор С, чтобы напряжение и сила тока совпадали по фазе? [С= 8,5 мкФ]

22. При подключении катушки индуктивности к батарее с напряжением 45 В через катушку течет ток 2,8 А. При ее подключении к источнику переменного напряжения 120 В, 60 Гц сила тока через катушку равна 4,6 А (эффективное значение). Определите индуктивность и активное сопротивление катушки. [54,5 мГн; 16 Ом]

23. Колебательный контур состоит из катушки индуктивностью 20 мкГн и конденсатора емкостью 80 нФ. Величина емкости может отклоняться от указанного значения на 2 %. Вычислите, в каких пределах может изменяться длина волны, на которую резонирует контур. [Δλ = 47,7 м]

24. Колебательный контур имеет индуктивность 1,6 мГн, емкость 0,04 мкФ и максимальное напряжение на зажимах 200 В. Чему равна максимальная сила тока в контуре? Сопротивление контура ничтожно мало. [1 А]

25. Как и какими индуктивностью L и С надо подключить катушку и конденсатор к резистору сопротивление R = 10 кОм, чтобы ток через катушку и конденсатор был в 10 раз больше общего тока? Частота переменного напряжения ν = 50 Гц. [3,18 Гн; 3,18 мкФ]

26. В колебательном последовательном контуре происходят вынужденные гармонические колебания. При частотах вынуждающей ЭДС ω₁ = 300 с^-1 и ω₂ = 600 с^-1 амплитуда силы тока равна половине своего максимального значения. Определить частоту ω₀ собственных гармонических колебаний контура и частоту ω_р вынуждающей ЭДС, при которой амплитуда напряжения на обкладках конденсатора максимальна. [424 с^-1; 406 с^-1]

27. Рассчитайте силу тока смещения между квадратными пластинами конденсатора со стороной 1,0 см, если напряженность электрического поля изменяется со скоростью 3,0∙10⁶ В/(м∙с). [2,7 нА]

28. Скорость накопления заряда на круглых обкладках плоского конденсатора емкостью 12,0 пФ составляет 12,0 мКл/с. Чему равна индукция магнитного поля на расстоянии 15,0 см по радиусу от центра конденсатора, если радиус обкладок равен 0,600 см? [0,016 мкТл]

29. Электрическое поле в плоской электромагнитной волне изменяется по закону Е_х=E₀cos (kz+ωt), Е_у= E_z=0. Определите: а) величину и направление вектора В, б) направление распространения волны.

[а) В=(E₀/c)cos(ωt + kу); б) в отрицательном направлении оси z]

30. Луч лазера мощностью 5,0 мВт имеет диаметр 2,0 мм. Чему равны среднеквадратичные значения Е и Вв луче лазера? [774 В/м; 0,258 мТл]

Контрольные вопросы третьего уровня (тесты)

1. Свободные незатухающие колебания заряда конденсатора в колебательном контуре описываются уравнением...
1.		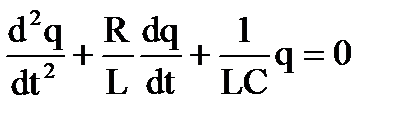2.
3.
2. Уменьшение амплитуды колебаний в системе с затуханием характеризуется временем релаксации. Если при неизменном омическом сопротивлении в колебательном контуре увеличить в 2 раза индуктивность катушки, то время релаксации...
1.	Увеличится в 2 раза	2.	Уменьшится в 4 раза
3.	Увеличится в 4 раза	4.	Уменьшится в 2 раза
3. Вынужденные колебания заряда конденсатора в колебательном контуре описываются уравнением...
1.		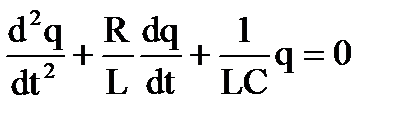2.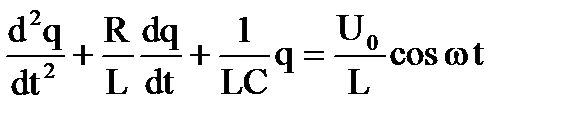
3.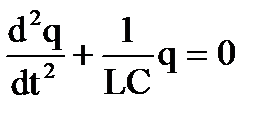
4. На рисунке представлена зависимость амплитуды колебаний напряжения на конденсаторе емкостью 1 нф, включенного в колебательный контур. Индуктивность катушки этого контура равна …
1.	1 мГн	2.	0,1 мГн	3.	10 мГн	4.	100 мГн
5. Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами A0.При разности фаз ∆φ = π амплитуда результирующего колебания равна...
1.	A0	2.	A0	3.	2A0	4.
6. Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами A0.При разности фаз ∆φ = π/2 амплитуда результирующего колебания равна...
1.		2.	2A0	3.	A0	4.	A0
7. Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет максимальную амплитуду при разности фаз, равной...
1.	p/2	2.	p	3.	p/4	4.
8.Колебательный контур состоит из последовательно соединенных емкости, индуктивности и резистора. К контуру подключено переменное напряжение (рис.). При некоторой частоте внешнего напряжения амплитуды падений напряжений на элементах цепи соответственно равны UR = 4 B, UL = 3 B, UC = 6 B. При этом амплитуда приложенного напряжения равна …	~ R L C E
1.	5 В	2.	13 В	3.	4 В		3 В
9. На рисунке представлена зависимость амплитуды колебаний напряжения на конденсаторе емкостью 1 нф, включенного в колебательный контур. Индуктивность катушки этого контура равна …
1.	1 мГн	2.	0,1 мГн	3.	10 мГн	4.	100 мГн

10. Колебательный контур состоит из катушки индуктивности L и конденсатора емкости С. Конденсатор заряжен до максимального напряжения U. Максимальная сила тока в контуре при свободных колебаниях в нем:

1) ; 2) ; 3) ; 4) ; 5) нет верного.

11. Колебательный контур состоит из катушки индуктивности (L = 50 мГн), конденсатора (С = 1 мкФ) и резистора сопротивлением R. При R = 1 Ом, логарифмический декремент затухания контура:

1) 0,14; 2) 1,4; 3) 14; 4) 0,0014; 5) 0,014.

12. Если для затухающих колебаний в колебательном контуре энергия колебаний уменьшается в n = 8 раз за N = 8 полных колебаний, то логарифмический декремент затухания контура:

1) 1,3; 2) 0,13; 3) 0,013; 4) 13; 5) 0,0013.

13. Декрементом затухания называется:

1) скорость затухания колебания; 2) величина b/2m;

3) отношение значений амплитуд, соответствующих моментам времени, отличающимся на период ;

4) отношение периодов двух последовательных колебаний;

5) величина bТ.

14. Установите правильную последовательность в изменении периода Т для свободных колебаний, совершаемых в среде с коэффициентом затухания b, равным: 1) b = 0, 2) b << w₀, 3) b = w₀, 4) b > w₀.

а) T 1> T 2> T 3> T 4;

б) T 1» T 2> T 3 >T 4;

в) T 1» T 2< T 3 <T 4;

г) T 1» T 2<< T 3 »T 4.

15. Приведите в соответствие физические величины их математическим выражениям.

Физическая величина	Математическое выражение
а) декремент затухания	1)
б) время релаксации	2)
в) добротность	3)
г) коэффициент затухания	4) b T

а);

б);

в);

г).

16. Установите соответствие между амплитудой и ее математическим выражением.

Амплитуда	Математическое выражение
а) незатухающих колебаний	1) A =
б) затухающих колебаний	2) A 0×e–b t ., b = 0
в) вынужденных колебаний	3) A 0×e–b t ., b > 0

а);

б);

в).

17. Установите правильную последовательность в изменении b для резонансных кривых, изображенных на рисунке.

b3

F 0/ k

О

А

w

w0

wрез

b2

b1

а) b1 > b2 > b3;

б) b1 > b2 < b3;

в) b1 < b2 > b3;

г) b1 < b2 < b3.

ЭЛЕКТРОМАГНЕТИЗМ
Введение
Лекция 1. Магнитное поле и его характеристики. Сила Ампера. Рамка с током в однородном магнитном поле. Закон Био-Савара-Лапласа и его применение для расчета магнитных полей. Взаимодействие двух параллельных проводников с током.
Контрольные вопросы первого уровня
Методические указания по решению задач
Примеры решения задач
Контрольные вопросы второго уровня (сборник задач)
Контрольные вопросы третьего уровня (тесты)
Лекция 2.Движение заряженных частиц в постоянных электрическом и магнитном полях. Теорема о циркуляции и ее применение для расчета поля соленоида и тороида.
Контрольные вопросы первого уровня
Примеры решения задач
Контрольные вопросы второго уровня (сборник задач)
Контрольные вопросы третьего уровня (тесты)
Лекция 3. Явление электромагнитной индукции. Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля в вакууме. Явление самоиндукции. Явление взаимной индукции. Энергия магнитного поля.
Контрольные вопросы первого уровня
Примеры решения задач
Контрольные вопросы второго уровня (сборник задач)
Контрольные вопросы третьего уровня (тесты)
Лекция 4. Электромагнитные колебания. Электрический колебательный контур. Формула Томсона. Свободные затухающие колебания. Добротность колебательного контура. Вынужденные колебания. Метод векторных диаграмм. Резонас напряжений и резонанс токов.
Контрольные вопросы первого уровня
Примеры решения задач
Контрольные вопросы второго уровня (сборник задач)
Контрольные вопросы третьего уровня (тесты)
Справочные данные
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ