Основные формулы. Собственная частота колебательного контура:

Собственная частота колебательного контура:

где L-индуктивность катушки; C-электроемкость конденсатора.

Дифференциальное уравнение свободных гармонических колебаний заряда в контуре и го решение:

где -амплитуда колебаний заряда конденсатора; 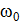-собственная частота контура.

Формула Томсона, устанавливающая связь между периодом T собственных колебаний в контуре без активного сопротивления, индуктивностью L и электроемкостью контура C:

Дифференциальное уравнение свободных затухающих колебаний в контуре и его решение:

,

где -амплитуда затухающих колебаний заряда конденсатора;

-начальная амплитуда; частота .

Добротность колебательного контура с активным сопротивлением R, индуктивностью L и электроемкостью контура C:

Дифференциальное уравнение вынужденных электромагнитных колебаний и его решение:

где ; -сдвиг по фазе между зарядом и приложенным напряжением .

Резонансная частота и резонансная амплитуда заряда в случае электрического резонанса:

где 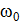-собственная частота контура; -коэффициент затухания; - амплитуда внешнего приложенного напряжения.

Реактивное индуктивное сопротивление (индуктивное сопротивление):

где - частота переменного напряжения, подаваемого на концы цепи.

Реактивное емкостное сопротивление (емкостное сопротивление):

Полное сопротивление цепи переменного тока, содержащей последовательно включенные резистор сопротивлением R, катушку индуктивностью L и конденсатор электроемкостью C:

Реактивное сопротивление:

Действующие (эффективные) значения силы тока и напряжения:

где и – амплитудные значения силы тока и напряжения.

Средняя мощность, выделяемая в цепи переменного тока:

Коэффициент мощности: