Исследование уравнения свободных колебаний

Рассмотрим уравнение свободных колебаний 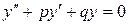, (1.1) где , ,

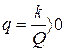k – коэффициент жесткости пружины,

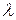- коэффициент, характеризующий силу сопротивления амортизатора.

Найдем общее решение дифференциального уравнения (1.1), для этого составим характеристическое уравнение 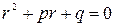, корни которого , .

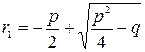1) Пусть или .

(Физический смысл задачи нам подсказывает, что это соответствует случаю, когда силы сопротивления амортизатора превосходят восстанавливающую силу пружины, интуитивно мы ожидаем, что колебаний груза не должно быть.)

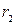Корни и - действительные числа, причем , .

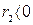Общее решение имеет вид .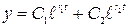

Из решения видно, что колебаний в данном случае действительно не будет.

При отклонение y стремиться к нулю, так как .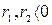

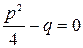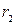2) Пусть или (сила сопротивления амортизатора присутствует, но она сравнима с силой действия пружины). В этом случае корни и действительные и равные .

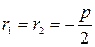Общее решение: .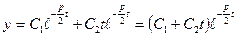

Здесь отклонение y так же стремиться к нулю при , однако не так быстро, как это было в предыдущем случае, благодаря наличию множителя .

3) Пусть 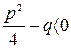или 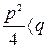(силы действия пружины превосходят силы действия амортизатора). Корни характеристического уравнения будут комплексными , где , .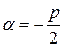

Общее решение дифференциального уравнения примет вид:

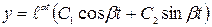(1.3)

Это решение представим в другом виде, заменив произвольные постоянные на 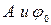связанные соотношениями:

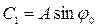, , отсюда

, .

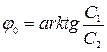Подставив в формулу (1.3) получим:

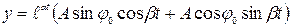или . (1.3)

Из решения (1.3) видно, что при , но в данном случае мы имеем дело с затухающими колебаниями.

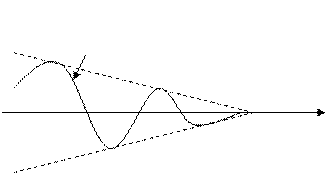
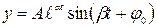
t

Предположим, что , т.е. отсутствует сила сопротивления, тогда общее решение уравнения (1.1) примет вид:

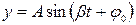(1.4)

Эти колебания называются гармоническими, и они появляются при отсутствии сил сопротивления:

А – амплитуда свободных колебаний;

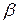- частота свободных колебаний;

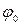- начальная фаза;

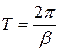- период колебаний (это промежуток времени, за который аргумент синуса изменяется на ).