Символічний метод

Вже можна передбачити, що при розрахунках кіл змінного струму необхідно буде використовувати складні перетворення з величинами, до яких входять тригонометричні функції, або виконувати графічні дії над векторами.

Найбільш ефективний метод розрахунку кіл змінного струму є символічний метод, оснований на зображенні електричних величин (струм, напруга, ЕРС, опори, провідності, потужності) комплексними числами. В цьому випадку для розрахунку кіл змінного струму можна використовувати закони Кірхгофа і всі методи розрахунку складних кіл постійного струму.

Нагадування про комплексні числа

Форми запису комплексних чисел

q В алгебраїчній формі комплексне число Z є сума дійсного числа a і уявного числа jb, тобто Z = a + jb. Уявне число jb є добуток уявної одиниці і коефіцієнта при ній b.

q Для зображення комплексного числа в графічній формі в прямокутній системі координат по горизонтальній осі відкладаються дійсні частини комплексного числа а, а по вертикальній осі – уявні частини jb. Комплексне число на такій комплексній площині зображується:

¨ точкою з координатами А (a; jb);

¨ вектором ОА, що починається в початку координат О, а закінчується в точці А з координатами (a; jb).

q Щоб записати комплексне число в показовій формі треба знати його модуль і аргумент. Модуль є довжина вектора ОА на комплексній площині

.

Аргумент – це кут a між додатним напрямком дійсної осі і вектором ОА. Ясно, що b/a = tg a, звідки a = arctg b/a.

При визначенні a треба мати на увазі, що обчислювальні засоби дають значення arctg b/a в межах 0°£ a £ 90°. Тому отримане значення треба відкоригувати згідно таблиці:

а	b	чверть	a
+	+	І	arctg b/a
–	+	ІІ	180° – arctg b/a
–	–	ІІІ	180° + arctg b/a
+	–	IV	– arctg b/a

Комплексне число в показовій формі є добуток модуля і множника е ^ja, тобто Z = |Z|× е ^ja.

q Тригонометрична форма. При розв’язанні задач комплексним методом виникає потреба перейти від показової форми до алгебраїчної. Вихідними є модуль і аргумент. Треба визначити дійсну і уявну частини і представити число в алгебраїчній формі.

З трикутника a = |Z|× cos a, b =|Z|× sin a.

В комплексній формі Z = a + jb = |Z|× cos a + j|Z|× sin a

Отриманий запис є тригонометричною формою комплексного числа.

Дії над комплексними числами

Для «+» і «–» зручніше використовувати алгебраїчну форму: Z 1 ± Z 2 = a 1 + jb 1 ± a 2 + jb 2 = (a 1± a 2) + j (b 1 ± b 2)

Для «´» і «:» зручніше використовувати показову форму: Z 1 ´ Z 2 = | Z 1 | e ja ´ | Z 2| e jb = | Z 1 | ´| Z 2| e j(a + b);

Z 1 / Z 2 = | Z 1 | e ja / | Z 2| e jb = | Z 1 | / | Z 2| e j(a – b),

але можна і алгебраїчну:

Z 1 ´ Z 2 = (a 1 a 2 – b 1 b 2) + j(a 1 b 2 + b 1 a 2); .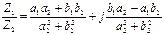

Два комплексних числа називаються спряженими, якщо відрізняються тільки знаками уявної частини (в алгебраїчній формі), або знаками аргументів (в показовій формі), наприклад:

a + jb та a – jb;

| Z| e ja та | Z| e –ja.

Уявлення параметрів електричного змінного струму через комплексні числа

Повертаючись до електричних величин можна провести аналогію між векторами, що обертаються і комплексними векторами. Ця аналогія дозволяє синусоїдальні величини відображувати комплексними числами. Комплексні значення струмів, напруг і ЕРС прийнято позначати .

Згадаймо вже знайомі кола з активним опором, індуктивністю і ємністю:

Побудуємо для цих кіл векторні діаграми, але вже на комплексній площині, вважаючи, що розташування вектора величини з нульовою початковою фазою співпадає з дійсною додатною піввіссю.

В усіх випадках вектор напруги 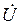направлений по осі дійсних чисел. Тому комплекс напруги , де U – модуль комплексу напруги, а 0° – його початкова фаза. Комплекс струму:

· у першому випадку –

· у другому випадку –

· у третьому випадку –

Отже комплексне зображення синусоїдальних величин визначає її діюче (амплітудне) значення і зсув фаз відносно вихідної величини, початкова фаза якої вважається рівною нулю.