 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Лекція 8. Трифазні кола
|
|
План
· Трифазна система ЕРС.
q Передмова. Розширення поняття фази.
q Принцип дії трифазного синхронного генератора. Трифазне коло.
q Уява електричних величин трифазних систем тригонометричними функціями, графіками, векторами, що обертаються, комплексними числами.
· Основні схеми з’єднання в трифазних колах
q Визначення лінійних та фазних величин. Співвідношення між лінійними та фазними струмами і напругами.
q Розрахунок трифазних кіл. Потужність трифазних кіл.
q Підсумок: комбінації з’єднань фаз джерела і споживача.
Трифазна система ЕРС.
Передмова
Широке впровадження змінного струму в промислові електроенергетичні установки почалось після 1891 року, коли російським вченим Доліво–Добровольським була розроблена, а потім практично освоєна система трифазного струму.
Трифазні кола є окремим випадком багатофазних систем змінного струму.
Багатофазними системами називають сукупність електричних кіл, в яких діють синусоїдальні ЕРС однакової частоти, такі, що відрізняються за фазою одна від одної і утворені в одному джерелі енергії (генераторі).
Кожне з однофазних кіл, що входять в багатофазну систему, прийняти називати фазою. Отже термін фаза в електротехніці позначає два різних поняття: 1) фазовий кут, що визначає миттєве значення синусоїдальної величини; 2) складову частину трифазного кола. Кола, в залежності від кількості фаз, називають двофазними, трифазними, шестифазними і т.п. До цього ми розглядали однофазні кола.
Найбільше розповсюдження в сучасній електроенергетиці отримали трифазні кола. Це пояснюється низкою переваг як перед іншими багатофазними колами, так і перед однофазними колами змінного струму. Серед переваг можна виділити такі:
· Економічність виробництва і передачі енергії в порівнянні з однофазними колами.
· Можливість простого отримання магнітного поля, що обертається, необхідного для роботи трифазних асинхронного та синхронного двигунів – одних з найрозповсюджених двигунів змінного струму.
· Можливість одночасного отримання в одній установці двох експлуатаційних номіналів напруг – фазної напруги і лінійної напруги.
Більш детально ці переваги (особливості) розглядатимуться далі.
Устрій генератора трифазного струму
Нагадаємо принциповий устрій генератора однофазного струму. Генератор змінного струму конструктивно складається з двох основних частин: ротора – частини, що обертається, і нерухомого статора. На роторі розташовані полюси N–S постійного магніту, як правило електромагніту, обмотка якого живиться від допоміжного джерела постійного струму невеликої потужності. Статор – сталевий циліндр, в повздовжніх пазах якого розміщені витки обмотки, в якій індукується змінна ЕРС.
На відміну від однофазного генератора в пазах статора трифазного генератора розміщені три однакові обмотки, зсунуті в просторі відносно одна одної на 120°. При обертанні ротора в кожній з обмоток статора індукується синусоїдальна ЕРС. Оскільки обмотки однакові, ЕРС, що в них утворюються будуть однакові за амплітудним значенням і частоті, але зсунуті за фазою відносно одна одної на 1/3 періоду. Виводи обмоток трифазного генератора прийнято позначати так: початки – буквами А, В, С, а відповідні їм кінці – X, Y, Z. Маркування виводів виконується з таким розрахунком, щоб індуковані в обмотках А–X, B–Y, C–Z ЕРС ` E A, ` E B, ` E C відставали на третину періоду ` E B від ` E A, ` E C від` E B.
Беручи за початок відліку моменти часу, коли ЕРС е А в обмотці А–Х дорівнює нулю можна записати такі вирази:
е А = Е m A sin w t;
е B = Е m B sin (w t – 120°);
е C = Е m C sin (w t – 240°).
Графіки цих ЕРС мають вигляд:
При символічній формі запису, якщо ЕРС фази А дорівнює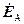 
, то ЕРС фаз В і С відповідно дорівнюють:
Векторна діаграма ЕРС 
уявлятиме собою симетричну трипроменеву зірку. Для такої зірки справедливе співвідношення 
. Таке ж співвідношення справедливе і для діючих значень 
.
Дійсно, з діаграми видно, що геометрична сума трьох векторів, рівних за величиною і зсунутих за фазою на третину періоду (120°) дорівнює нулю. Сума миттєвих значень ЕРС трифазного генератора в будь–який момент часу також дорівнює нулю е А + е В + е С = 0.
Незв’язана система трифазних струмів
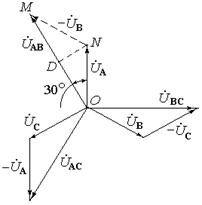
Якщо до кожної з обмоток трифазного генератора через два проводи приєднати навантаження – опори Z A, Z B, Z C, то утворюються три електрично незв’язані однофазні кола.
на клемах навантаження рівні за величиною і зсунуті за фазою відносно одна одної на третину періоду. Величину струмів, а також коефіцієнт потужності (cos j) в кожному з трьох кіл можна знайти за формулами:
Позначені на малюнку напрямки струмів і ЕРС є загальновживаними.
Незв’язане трипроводне коло потребує для живлення трьох окремих навантажень шість окремих проводів і, отож, економія в проводах в порівнянні з однофазним колом не досягається. Така система на практиці не використовується.
Основні схеми з’єднання в трифазних колах
З’єднання за схемою «зірка»
Чотирипровідна система. Якщо об’єднати кінці обмоток генератора в спільну точку О, а кінцеві клеми навантажень в спільну точку О¢, то для з’єднання генератора і трьох навантажень потрібно буде всього чотири проводи.
Точки О, О' називають відповідно нульовою (нейтральною) точкою генератора і нульовою (нейтральною) точкою навантаження.
Проводи А–А, В–В, С–С називають лінійними, а провід О–О' – нульовим або нейтральним. Отримана схема має назву чотирипровідна система трифазного струму, або з’єднання зіркою з нульовим проводом.
Напруга між лінійним проводом і нульовим має назву фазна напруга і позначається U A, U B, U C.
Напруга між лінійними проводами називається лінійною напругою і позначається U AВ, U BС, U СА.
До навантажень Z A, Z B, Z C прикладені фазні напруги.
В трифазних колах розрізняють лінійні І л і фазні І Ф струми.
Лінійними називають струми І А, І В, І С, щопротікають по лінійних проводах.
Струми, що протікають по обмотках генератора, або по опорах навантаження називають відповідно фазними струмами генератора і фазними струмами навантаження.
При з’єднанні зіркою лінійний струм рівний фазному І л = І Ф.
Струм, що протікає по нульовому проводі, позначають І N.
Заміна незв’язаної шостипровідної системи чотирипровідною не впливає на величину фазних напруг генератора, тому струми І А, І В, І С при тій і другій системі залишаються однаковими (якщо не враховувати опір проводів).
Формули (1) залишаються справедливими і для чотирипровідної системи.
Застосувавши до нульової точки О' перший закон Кірхгофа і прийнявши позначені на схемі напрямки струмів за додатні, отримаємо:
або
тобто струм в нульовому проводі визначається сумуванням лінійних струмів в комплексній формі, або геометричним сумуванням векторів ` І А, ` І В, ` І С.
На малюнку стрілками показані додатні напрямки фазних напруг на опорах навантаження. Миттєва напруга, наприклад напруга u AB, між лінійними проводами А і В дорівнює алгебраїчній сумі миттєвих напруг на ділянці кола між точками А і В:
u AB = u A + (–u B)
В цьому виразі напругу u B взято із знаком «–» оскільки напрям дії цієї напруги протилежний прийнятому напряму обходу кола від точки А до точки В. Теж саме в діючих значеннях:
.
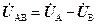Аналогічно для лінійних напруг: 
і 
:
Векторна діаграма напруг буде мати вид:
З діаграми видно, що всі три лінійні напруги рівні між собою за величиною і зсунуті за фазою відносно одна одної на 120°.
З трикутника OMN маємо:
OM = 2×OD = 2×ON×cos 30° = 
×ON.
Оскільки ОМ = U AB = U л; ON = U A = U Ф, то U л = × U Ф, тобто миттєва напруга при з’єднанні зіркою в разів більша за фазну.
В трифазних установках навантаження окремих фаз прагнуть зробити більш–менш однаковим. При цьому струм в нульовому проводі виявляється меншим кожного з лінійних струмів. Виходячи з цього перетин нульового проводу приймають рівним приблизно половині перетину лінійного проводу. Це веде до суттєвого зниження загальної ваги проводів чотирипровідної системи в порівнянні з незв’язаною шестипровідною.
Трипровідна система. При симетричному (рівномірному) навантаженні фаз, тобто, коли опори навантажень однакові Z A = Z B = Z C вектори струмів в усіх фазах рівні за величиною і зсунуті відносно своїх напруг на один і той же кут j.
Векторна діаграма в цьому випадку має вид:
Сума лінійних струмів дорівнює нулю, а отже струм в нульовому проводі відсутній (І N = 0).
При симетричному навантаженні відпадає необхідність в нульовому проводі і передачу енергії від генератора до споживачів можна здійснювати по трьом проводам.
Схема трипровідної передачі має вигляд:
Електричні мережі виконуються трипровідними тільки для живлення таких споживачів, кожний з яких створює симетричне навантаження всіх трьох фаз.
Напруги між лінійними проводами практично залишається рівними за величиною (U AВ = U BС = U СА) і взаємно зсунуті по фазі на 120° як при симетричному так і при несиметричному навантаженні фаз. Фазні ж напруги в трипровідній мережі однакові за величиною тільки у випадку симетричного навантаження фаз.
Якщо в цій мережі через будь–які обставини порушується рівномірність навантаження окремих фаз, то напруга між нульовою точкою навантаження і лінійними проводами, тобто фазні напруги споживачів U A, U B, U C будуть неоднакові. В зв’язку з цим встановлене раніше співвідношення U л = × U Ф для трипровідної системи справедливе тільки при симетричному навантаженні фаз.
Як приклад наведемо схему чотирипровідної мережі для живлення триповерхового будинку і схему трипровідної мережі для живлення групи трифазних двигунів:
На малюнках вказані місця встановлення плавких запобіжників для захисту мережі від перенавантаження і коротких перемикань.
Треба відмітити недопустимість встановлення запобіжників в нульовому проводі, так як перегоряння цього запобіжника у випадку несиметричного навантаження фаз призведе до підвищення напруги на навантаженні в одній, або двох фазах.
Потужність трифазного кола.
Потужність трифазного кола при з’єднанні зіркою. Активні і реактивні потужності в кожній з фаз трифазної системи можна знайти за формулами:
P A = U A I AcosjA P B = U B I BcosjB P C = U C I CcosjC
Q A = U A I AsinjA Q B = U B I BsinjB Q C = U C I CsinjC
Загальна потужність трифазної системи (активна і реактивна) визначається сумою потужностей окремих фаз: P = P A + P B + P C; Q = Q A + Q B + Q C.
При симетричному навантаженні: P A = P B = P C = P ф; Q A = Q B = Q C = Q ф; jA = jB = jC = j. Тоді:
P = 3× P ф = 3× U ф I фcosj
Q = 3× Q ф = 3× U ф I фsin j
S = 3× U ф I ф
Ці формули визначають потужність трифазної системи через фазні струми і напруги.
Іноді буває зручніше вираховувати потужність через лінійні величини струмів і напруг. Враховуючи, що при з’єднанні зіркою І л = І Ф і U л = × U Ф, отримаємо
P = × U л I лcosj
Q = × U л I лsin j
S = × U л I л
Розрахунок трифазного кола.
Трипровідна система із симетричним навантаженням.
При симетричному навантаженні фаз (Z A = Z B = Z C = Z) розрахунок трифазного кола зводиться до розрахунку однофазного кола.
За заданим U л визначають фазну напругу U ф = U л / 
, а потім за відомим опором навантаження Z визначають струм в проводах живлення I л = I ф = U ф / Z. Зсув фаз між струмом і фазною напругою визначають за формулою cosj = R / Z. Потужність визначається за вище наведеними формулами. Векторна діаграма вже була побудована.
Приклад. До трифазної мережі з лінійною напругою U приєднаний двигун, обмотки якого з’єднані зіркою. Споживана потужність двигуна Р при cosj. Визначити:
1) діюче значення споживаного струму І;
2) реактивну потужність Q, споживану двигуном;
3) миттєві значення струмів в кожній з фаз для різних моментів часу.
Розв’язання. Діюче значення струмів 
.
Реактивна потужність 
.
Миттєві значення струмів і А, і В, і С:
а) для моменту часу, коли струм фази А досягає додатного максимуму
і А = І m = I л 
; i B = I m ×sin(–30°) = I л ×sin(–30°); i C = I m ×sin(–150°) = I л ×sin(–150°).
б) для моменту часу, коли струм фази А проходить через нуль
і А = 0; i B = I m ×sin 60° = I л ×sin 60°; i C = I m ×sin(–60°) = I л ×sin(–60°).
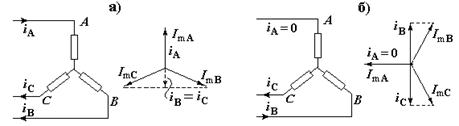
Чотирипровідна система при несиметричному навантаженні.
Струм для кожної фази:
Для визначення струму в нульовому проводі можна побудувати векторну діаграму, або використати для зображення електричних величин комплексні числа.
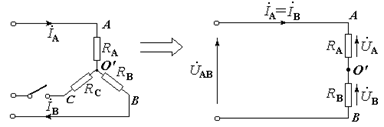
Приклад. U л = 220 в; R A = 10 Ом; R В = 5 Ом; R С = 7,5 Ом. Визначити:
1) лінійні струми І А та І В;
2) фазні напруги U А та U В ,
якщо нульовий провід відсутній, а навантаження R С відключене.
Розрахунок:
При відключенні R С навантаження R A і R В утворюють послідовне однофазне коло. Струм в опорі R С дорівнює 0. Тоді І А = І В = U АВ / (R A + R В) = 220 / (10 + 5) = 14,7 A.
U А = І А × R A = 14,7×10 = 147 [в]; U В = І В × R В = 14,7×5» 73 В.
Отриманий результат показує, що фазні напруги U А на опорі R A підвищилась в порівнянні з номінальним режимом (коли U Ф = U л / = 220 / = 127 В). Якщо б в фазу А були включені електричні лампи, розраховані на номінальну напругу 127 в, то при відсутності нульового проводу вони б знаходились під дією підвищеної напруги (147 в) і швидко б вийшли з ладу. Неприпустимо встановлення запобіжника в нульовому проводі.
Методика розрахунку з використанням комплексних чисел.
При значній нерівномірності навантаження окремих фаз і особливо при відсутності нульового проводу симетрія напруг у споживачів порушується. В таких випадках, коли розрахунок трифазної системи не можна звести до розрахунку кіл окремих фаз з однаковими за величиною напругами, використовують символічний метод. Розглянемо схему чотирипровідної системи з урахуванням опорів проводів:
Чотирипровідну систему можна розглядати як складне коло з двома вузлами О і О' і для розрахунку застосувати метод вузлових напруг.
Позначимо:
– фазні напруги на клемах генератора;
– фазні напруги на клемах навантажень;
– повні опори окремих фаз, включаючи опори лінійних проводів;
– повні провідності окремих фаз;
– опір нульового проводу;
– провідність нульового проводу.
Вважаємо, що вузловий потенціал в вузлі О дорівнює нулю. Тоді рівняння для вузла О', складене за методом вузлових напруг буде мати вид:
Вузлова напруга, тобто напруга між нульовою точкою навантаження О' і нульовою точкою генератора О, визначається за формулою:
Далі, за методом вузлових напруг визначаються струми в вітках, тобто струми в нульовому і лінійних проводах:
Напруги на опорах навантаження:
Нехтуючи опором лінійних проводів за попередніми формулами отримуємо співвідношення між фазними напругами генератора і навантаження:
Нагадуємо, що при симетричному навантаженні напруга U N між нульовими точками генератора і навантаження дорівнює нулю, оскільки діючі напруги U А, U В, U С на клемах навантаження однакові за величиною і зсунуті за фазою на третину періоду.
Приклад. В чотирипровідну мережу трифазного струму з лінійною напругою U л = 220 В включені зіркою три групи ламп з опором R А = 10 Ом, R В= 5 Ом, R С = 7,5 Ом. Визначити фактичні напруги на клемах ламп, що включені в фази А, В, С при обриві нульового проводу.
Розрахунок:
Оскільки опір лінійних проводів малий в порівнянні з опором ламп, можна вважати Z A » R А = 10 Ом, Z B » R В= 5 Ом, Z С » R С = 7,5 Ом.
Нехай вектор 
спрямований по дійсній осі. Тоді для фазних напруг джерела можна записати:
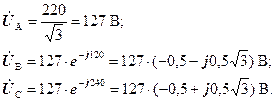
Провідність окремих фаз:
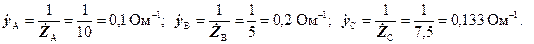
При відсутності нульового проводу 
.
Напруга між точками О і О':
Фазні напруги на клемах навантаження:
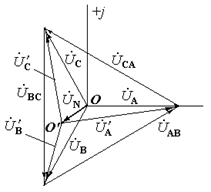Напруги U A ' і U С ' на менш завантажених фазах перевищують номінальну напругу ламп, тому лампи, включені в фази А і С, можуть швидко перегоріти.
Векторна діаграма матиме вид:
Вихідна точка О відповідає нульовій точці генератора, а кінці векторів 
– точкам А, В, С кола. Від точки О відкладаємо вектор 
, кінець якого О' відповідає нульовій точці О' навантаження. Відрізки, що з’єднують на діаграмі точку О' з кінцями векторів 
уявляють собою вектори напруг 
. Вектори 
зображують лінійні напруги кола.
При симетричному навантаженні точка О' співпадає на діаграмі з початком векторів О. При виникненні несиметрії навантаження точка О' зміщується відносно початку векторів О. Це явище має назву зміщення нейтралі.
Опір нульового проводу, як правило в багато разів менше опору навантаження будь–якої з фаз, тобто провідність нульового проводу y Nзначно перевищує провідність окремих фаз y А, y В, y С. Це значить, що при наявності нульового проводу величина 
зменшується в кілька разів, і фазні напруги 
в цих умовах утворюють трифазну систему, достатньо близьку до симетричної.
З’єднання за схемою “трикутник”
З’єднання споживачів за схемою “трикутник”.
Якщо мережу трифазного струму між кожною парою лінійних проводів А–В, В–С, С–А включити три опори Z AB, Z BC, Z CA, то під дією лінійних напруг в кожному з цих опорів почне протікати струм. Такий спосіб включення опорів в трифазну мережу має назву включення трикутником.
При з’єднанні навантажень «трикутником» по їх опорам протікають струми I AB, I ВC, I CA. Ці струми називають фазними. Струми I A, I В, I C, що протікають в лінійних проводах мережі називають лінійними. Показані на малюнку напрямки струмів є додатними загальноприйнятими напрямками.
Напруга, що прикладена до опорів навантажень Z AB, Z BC, Z CA прийнято називати фазними напругами U ф. В наведеній схемі фазна напруга дорівнює напрузі між лінійними проводами, тобто лінійній напрузі U л. Тому при з’єднанні «трикутником» U л = U ф.
Вибір схеми з’єднання споживачів вирішується в залежності від величини лінійної напруги мережі і номінальної напруги споживачів. В трифазних установках можливі випадки, коли одна частина споживачів з’єднана «зіркою», а інша – «трикутником».
При заданій величині лінійної напруги U л = U ф, відомих значеннях опорів навантаження можна розрахувати фазні струми і коефіцієнти потужності окремих фаз:
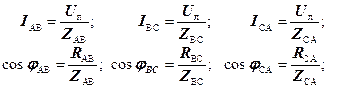
Для встановлення співвідношень між лінійними і фазними струмами складаються рівняння за першим законом Кірхгофа для точок розгалуження А, В, С, враховуючи вибрані додатні напрямки струмів:
Звідки:
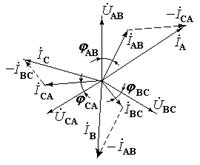
З отриманих виразів випливає, що кожний вектор лінійного струму дорівнює різниці векторів відповідних фазних струмів.
Векторна діаграма напруг 
, фазних струмів 
і лінійних струмів 
має вид:
Складаючи праві і ліві частини рівнянь (1) отримаємо 
, тобто геометрична сума лінійних струмів дорівнює нулю як при симетричному, так і при несиметричному навантаженні.
При симетричному навантаженні
;
j AB = j BC = j CA = j.
В цьому випадку лінійні струми рівні між собою 
і утворюють правильну трипроменеву зірку. Із рівнобедреного трикутника OMN можна знайти співвідношення між величинами лінійного і фазного струмів. При симетричному навантаженні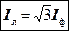 
.
Потужність трифазного кола при з’єднанні навантажень «трикутником». В цьому випадку потужність визначається за тими же формулами, що і при з’єднані «зіркою».
Потужність окремих фаз:
P AB = U AB× I AB×cos jAB Q AB = U AB× I AB× sin jAB
P BC = U BC× I BC×cos jBC Q BC = U BC× I BC× sin jBC
P CA = U CA× I CA×cos jCA Q CA = U CA× I CA× sin jCA
Загальна потужність трифазної системи визначається сумою потужностей окремих фаз
Р = P AB + P BC + P CA
Q = Q AB + Q BC + Q CA
При симетричному навантаженні потужності окремих фаз рівні між собою, отже
Р = 3× Р ф = 3× U ф ×I ф × cos j; Q = 3× Q ф = 3× U ф ×I ф × sin j; S = 3× U ф ×I ф
Враховуючи, що при з’єднанні «трикутником» U л = U ф і 
, можна отримати вирази потужностей через величини лінійних струму і напруги:
Р = 
× U л ×I л × cos j
Q = × U л ×I л × sin j
S = × U л ×I л
На практиці буває необхідно переключити опори навантаження із схеми “трикутник” на схему “зірка”, наприклад, переключення трифазних електропечей з метою регулювання їх потужності, а, відповідно і температури. Потужність, що споживається при з’єднанні “трикутником”, буде при тій же напрузі мережі в тричі більшою за потужність, що споживається цими ж опорами при з’єднанні “зіркою”. Дійсно, при з’єднанні “зіркою”
,
а при з’єднанні “трикутником”
, звідки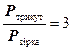 
.
З’єднання обмоток генератора за схемою «трикутник».
З’єднання «трикутником» – це коли початок кожної фазної обмотки з’єднується з кінцем наступної по порядку фазної обмотки так, що всі три обмотки утворюють замкнутий контур. В цьому контурі напрямки фазних ЕРС е А, е В, е С співпадають.
До клем А, В, С приєднується трифазна мережа, що живить навантаження. Лінійні напруги між кожною парою клем дорівнює фазній напрузі джерела (U л = U ф).
При відсутності навантаження струм в контурі генератора АВСА не виникає, оскільки результуюча ЕРС (сумарна 
) в контурі в будь–який момент часу дорівнює нулю.
Звичайно, обмотки електромашинних генераторів з’єднують зіркою. Обмотки трифазних трансформаторів, від яких живляться споживачі, прийнято з’єднувати як “зіркою”, так і “трикутником”.
Комбінації з’єднань фаз джерела і споживача.
З’єднання «зірка – зірка»
Це з’єднання зазвичай використовують тоді, коли номінальна фазна напруга генератора дорівнює номінальній фазній напрузі споживачів.
Лінійні струми в такій системі дорівнюють фазним струмам споживачів:
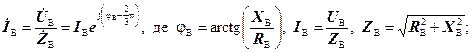
В нейтральному проводі протікає струм .
Якщо навантаження симетричне, то 
і нейтральний провід може бути відключений.
Якщо навантаження не симетричне, то 
і тоді наявність нейтрального проводу є обов’язковою, оскільки його відсутність впливає на значення фазних напруг споживача – на менш завантажених фазах фазна напруга перевищуватиме номінальну.
З’єднання «зірка – трикутник»
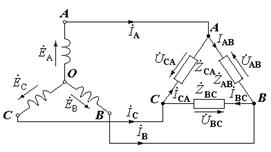В цьому випадку фази генератора з’єднуються за схемою «зірка», а фази споживача – «трикутником», тобто навантаження споживача включені безпосередньо між лінійними проводами. Така схема використовується у випадку, коли номінальна напруга живлення споживача більша фазної напруги генератора в 
раз. Нейтральний провід при такому способі з’єднання завжди відсутній.
Струми в кожній із фаз визначаються співвідношеннями:
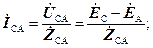
Визначення фазних струмів в навантаженнях спживачів можна здійснити через активні і реактивні складові комплексних опорів 
. Так, наприклад, для струму 
маємо модуль:
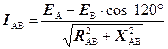
і фазовий зсув
Аналогічно визначаються I BC, і φBC та I CA, і φCA.
Лінійні струми та фазні струми генератора 
через фазні струми споживачів визначаються співвідношеннями:
Як випливає із наведених співвідношень лінійні струми в системі «зірка – трикутник» завжди бульше струмів в фазах споживача (при симетричному навантаженні 
).
З’єднання «трикутник – трикутник»
Таке з’єднання використовується в тому випадку, коли номінальна напруга фаз споживача дорівнює фазній напрузі генератора і за вимогами техніки безпеки лінійна напруга не може перевищувати фазну напруга генератора.
На відміну від з’єднання фаз генератора «зіркою», де 
, при такому способі з’єднання завжди U л = U ф. Нейтральний провід в такій системі відсутній.
Нехтуючи опором проводів маємо:
Струми фаз споживача розраховуються за формулами:
де 
і т.д.,
а струми в лінійних проводах:
Лінійні струми, як і попередній системі, перевищує фазні струми споживача і при симетричному навантаженні 
.
Очевидно, що при одній і тій же споживаній потужності зниження лінійної напруги зумовлює збільшення струмів в лінійних проводах. Тому при можливості збільшення лінійної напруги слід уникати такого способу підключення споживачів.
З’єднання «трикутник – зірка»
Таке з’єднання використовується в тому випадку, коли споживач має номінальну напругу живлення фази в раз меншу, ніж лінійна напруга на виході генератора (наприклад, якщо U A = U B = U C = 220 В, а U ф.ном = 127 В). Нейтральний провід при цьому відсутній.
При такому з’єднанні:
Як і в системі «зірка – зірка», фазні напруги навантаження менше лінійних напруг (зокрема, при симетричному навантаженні в раз).
Дата публикования: 2014-11-04; Прочитано: 11189 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
