 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Лекція 6. Аналіз кіл синусоїдального струму
|
|
План
· Розрахунок кіл синусоїдального струму.
q Закони Кірхгофа для кіл синусоїдального струму.
q Кола з послідовним з’єднанням резистора та котушки індуктивності, резистора та конденсатора.
q Кола з послідовним з’єднанням віток.
q Трикутник опорів та потужностей.
q Розрахунок складних кіл змінного струму.
q Коефіцієнт потужності та його техніко-економічне значення.
Розрахунок кіл синусоїдального струму.
Закони Кірхгофа
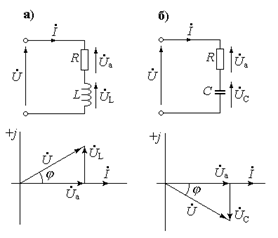
Розрахунок кіл синусоїдального змінного струму оснований на використанні законів Кірхгофа, які справедливі для миттєвих, амплітудних та діючих значень:
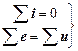 для миттєвих значень – суми алгебраїчні.
для миттєвих значень – суми алгебраїчні.
|
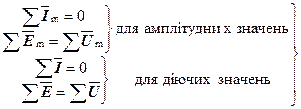
|
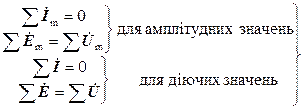
Розглянемо кола:
В обох випадках вектор струму 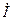 направлений по осі дійсних чисел. Комплекс напруги на клемах кола:
направлений по осі дійсних чисел. Комплекс напруги на клемах кола:
· для випадку а) 
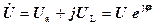 , де U a і jU L – дійсна і уявна частини; U і j – модуль і початкова фаза комплексу напруги.
, де U a і jU L – дійсна і уявна частини; U і j – модуль і початкова фаза комплексу напруги.
· для випадку б) 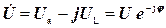 .
.
В загальному виразі комплексу напруги “+” перед уявною частиною свідчить, що навантаження має індуктивний характер, “–“ – характер навантаження ємкісний.
Розглянемо електричне коло, що складається з трьох елементів:
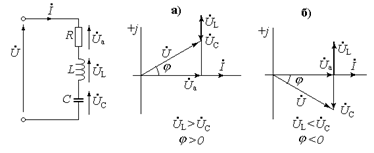 |
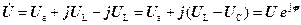 , де
, де 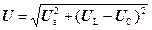 , а аргумент
, а аргумент 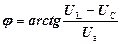 .
.
j > 0, якщо U L > U C
j < 0, якщо U L < U C.
Опір і провідність в комплексній формі.
Розрізняють повний опір Z, реактивний опір X і активний опір R, а також відповідні їм провідності: повна провідність – y = 1 /Z, реактивна провідність – b = X / Z 2 і активна провідність – g = R / Z 2.
З розглянутих трикутників напруг (наприклад, а) і б)) 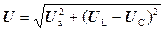 =
=
= 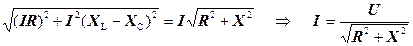 . Це відношення є законом Ома. Величина
. Це відношення є законом Ома. Величина 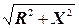 – повний опір кола і позначається Z.
– повний опір кола і позначається Z. 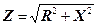 . Тобто I = U / Z.
. Тобто I = U / Z.
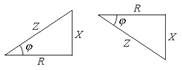 Активний, реактивний і повний опір пов’язані між собою як сторони трикутника.
Активний, реактивний і повний опір пов’язані між собою як сторони трикутника.
Ці трикутники можна побудувати на комплексній площині і тоді опори можна виразити комплексними числами:
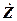 = R + j X = R + j(X L – X C), де
= R + j X = R + j(X L – X C), де 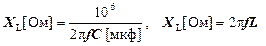 .
.
Аналогічно визначаються провідності: 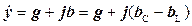 .
.
При записі повної провідності в показовій формі:
модуль комплексу опору – 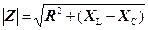 ; аргумент –
; аргумент – 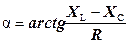 .
.
Активна, реактивна і повна потужність.
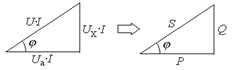 Якщо сторони трикутника напруг помножити на струм І, то отримаємо трикутник потужностей:
Якщо сторони трикутника напруг помножити на струм І, то отримаємо трикутник потужностей:
Активна потужність – P = U a ×I = UI× cos j[вт];
Реактивна потужність – Q = U L / C ×I = UI× sin j[вар];
Повна потужність – S = U×I [в × а].
Розрахунок складних кіл змінного струму.
Формули законів Ома і Кірхгофа для кіл змінного струму в комплексній формі мають таку ж структуру, як і для кіл постійного струму. Тому методи розрахунку лінійних кіл постійного струму, що були вже розглянуті (метод безпосереднього використання законів Кірхгофа, метод суперпозиції, метод контурних струмів, метод вузлових потенціалів, метод еквівалентного генератора), можна застосовувати для розрахунку складних лінійних кіл синусоїдального змінного струму. В цьому випадку всі ЕРС, напруги, струми, опори і провідності ділянок кола визначаються так же, як і в колах постійного струму, але в комплексній формі.
Значення cos j.
Електроприймачі змінного струму є або пристроями, що споживають тільки активну потужність (лампи розжарювання, електронагрівальні прилади – печі, праски), або пристрої, що споживають як активну, так і реактивну потужність (зокрема двигуни змінного струму).
Активна потужність, що споживається двигуном, перетворюється ним в корисну механічну роботу і частково розсіюється у вигляді тепла.
Разом з необратним перетворенням електроенергії в інші види енергії тут одночасно проходить обратний процес обміну енергією між змінним магнітним полем і джерелом живлення.
Якщо б двигун отримував від джерела тільки активну потужність Р, тобто працював би з cos j = 1, то споживав би струм I = P / U. В дійсності двигун змінного струму є для джерела як активним, так і реактивним навантаженням, тобто працює з індуктивним cos j. В зв’язку з цим двигун при тій же активній потужності Р і, відповідно, при тій же корисній механічній роботі споживає з мережі струм більшої величини 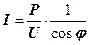 .
.
Зниження cos j призводить:
1. до підвищення втрат електроенергії (I 2 Rt) в проводах лінії;
2. до завищення необхідної потужності (S = UI) джерела живлення.
Так, наприклад, якщо двигун працює з cos j = 0,7, то втрати енергії в лінії збільшується пропорційно (1/ cos j) 2, тобто в 2 рази, а потужність джерела повинна бути більшою майже в 1,5 рази в порівняння з роботою при cos j = 1.
Якщо паралельно двигуну включити конденсатор такої ємності, щоб реактивна складова загального струму стала рівною нулю, то загальний cos j кола буде дорівнювати 1. У випадку повної компенсації конденсатор цілком покриває потреби двигуна в реактивній потужності і із мережі буде споживатись тільки активна потужність Р.
Для усвідомлення значення cos j звернемось до основних характеристик генератора: номінальні напруга U ном, струм I ном, потужність S ном = U ном × I ном. U ном = 1200 В, I ном = 200 А. Тоді S ном = U ном × I ном = 1200 × 200 = 240 кВ × А. Будемо приєднувати навантаження з різними cos j.
Для активного навантаження cos j = 1, активна потужність генератора Р = U ном × I ном = 240 квт, тобто дорівнює повній потужності.
Для навантаження з cos j = 0,5 активна потужність генератора Р = U ном × I ном × cos j = 1200 × 200 × 0,5 = 120 квт, тобто знижується в 2 рази. Не зважаючи на це по генератору і проводах проходить той же струм 200 А. Тобто генератор працює з повною потужністю. Активна потужність генератора зменшилась за рахунок збільшення реактивної потужності, що без користі завантажує генератор і лінію електропередачі.
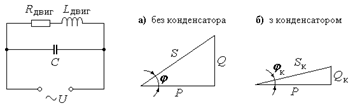 |
До підключення конденсатора Q = P× tg j.
З конденсатором Q к = P× tg j к.
Реактивна потужність, яку повинен сприйняти конденсатор
Q С = Q – Q к = Р× (tg j – tg j к). З іншого боку 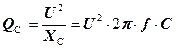 . Звідки:
. Звідки:
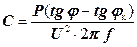 .
.
Для повної компенсації реактивної потужності (j к = 0) необхідний конденсатор ємкістю 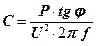 .
.
Дата публикования: 2014-11-04; Прочитано: 2337 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
