Волновая функция

Итак, микрочастицы не подчиняются законам классической механики, их поведение нельзя описать принятыми в классической физике способами. Этот факт заставил ученых создать новую теорию. Новая механика, названная квантовой, основывалась на идеях Планка, Эйнштейна, Борна и де Бройля. Основоположниками стали австриец Эрвин Шредингер (1887 – 1961), немец Вернер Карл Гейзенберг (1901 – 1976) и англичанин Поль Адриен Морис Дирак (1902 – 1984).

Одной из основных при этом стала задача математического описания поведения микрочастиц, причем такое, чтоб характеризующая их функция отражала одновременно и волновые и корпускулярные свойства.

Рассмотрим картину, образующуюся при дифракции электронов на двух щелях. В каждой точке фотопластинки степень почернения, вызванного ударами дифрагированных электронов, определяется интенсивностью волн де Бройля в направлении данной точки (рис. 4.2). Напомним, что согласно волновой теории света, число фотонов в данной точке дифракционной картины задается квадратом амплитуды световой волны, то есть ее интенсивностью. С другой стороны, число электронов в каждой точке дифракционной картины определяется вероятностью их попадания в данную точку. Чтобы учесть волновые свойства микрочастиц, де Бройль предложил рассматривать некую функцию Ψ(x,y,z,t), меняющуюся по волновому закону, т.е. как волну де Бройля (см. выше):

(4.11)

где – вектор, определяющий положение частицы в пространстве. Ψ(x,y,z,t) была названа волновой функцией.

Идея использовать функцию вида (4.11) возникла в связи с тем, что поведение свободной микрочастицы имело выраженную аналогию с поведением световой волны, описываемой волновыми уравнения колебаний векторов электрической и магнитной напряженностей:

(4.12)

где для учета корпускулярных свойств волновые параметры и заменены с учетом формул (4.1, 4.2) энергией и импульсом рассматриваемой частицы:

(4.13)

Однако, не следует думать, что волновая функция получена простой подстановкой соответствующих параметров в выражения (4.12). Она лишь имеет аналогичную формулировку и отражает корпускулярно-волновые особенности как поведения микрочастиц, так и распространения света.

Правильную интерпретацию волновой функции дал М. Борн в 1926 г. Сама волновая функция имеет комплексное значение и не обладает физическим смыслом – то есть в природе не существует такого параметра, измерение которого дало бы значение, равное волновой функции.

Согласно Борну, физический смысл имеет квадрат модуля волновой функции, который пропорционален вероятности обнаружить частицу в момент времени t в объеме dV (dx, dy, dz) вокруг точки (x, y, z):

(4.14)

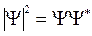(4.15)

где Ψ^* – функция, комплексно сопряженная с Ψ.

Таким образом, в квантовой механике вводится так называемая волновая функция, которая полностью описывает состояние микрочастицы и при этом отражает как ее корпускулярные, так и волновые свойства.

Вероятность обнаружить частицу в элементе объема dV равна:

(4.16)

Вероятность же нахождения частицы в конечном объеме V, согласно теореме сложения вероятностей, равна:

(4.17)

где интегрирование проводится по координатам x, y, z. Очевидно, что сам факт существования частицы означает, что вероятность найти ее где-либо в бесконечном объеме равна 1:

(4.18)

Выражение (4.18) называется условием нормировки волновой функции.

Волновая функция Ψ (x, y, z, t) является комплексной, конечной (в противном случае вероятность обнаружения частицы может оказаться больше 1), однозначной и непрерывной. Забегая вперед, уточним, что непрерывными должны быть и частные производные , , , .

Кроме того, волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями Ψ₁, Ψ₂,..., Ψ_n,..., то она может находиться в состоянии Ψ, описываемом линейной комбинацией этих функций:

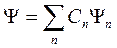(4.19)

где C_n (n = 1, 2,...) – произвольные комплексные числа.

С помощью волновой функции можно найти средние значения физических величин, таких как средние скорость, расстояние электрона от ядра и другие. В частности средняя скорость частицы будет равна:

(4.20)