 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Властивості векторного добутку
|
|
1. 
 .
.
Справедливість цієї властивості випливає з означення.
2. 
 .
.
Доведення. Нехай 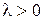 . Вектор
. Вектор  перпендикулярний векторам
перпендикулярний векторам  і
і  (вектори
(вектори  і
і  лежать в одній площині). Вектор
лежать в одній площині). Вектор  також перпендикулярний векторам
також перпендикулярний векторам  і
і  . Отже, вектори
. Отже, вектори  і
і  колінеарні. Очевидно, що їх напрямки співпадають. Вони мають однакову довжину:
колінеарні. Очевидно, що їх напрямки співпадають. Вони мають однакову довжину:
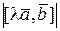

 і
і 


 .
.
Тому 
 . Аналогічно доведення при
. Аналогічно доведення при  .
.
3.  .
.
Приймемо без доведення.
4. Два ненульові вектори  і
і  колінеарні тоді і тільки тоді, коли їх векторний добуток рівний нульовому вектору, тобто
колінеарні тоді і тільки тоді, коли їх векторний добуток рівний нульовому вектору, тобто 

 .
.
Доведення. Якщо  , то вектор
, то вектор  за означенням.
за означенням.
Якщо  , то
, то  . Тоді
. Тоді 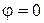 або
або  , тобто
, тобто  .
.
Приклад 6.8. Знайти площу паралелограма, побудованого на векторах  і
і  , якщо
, якщо  ,
,  ,
,  ,
,  ,
,  .
.
Розв’язок. Використовуючи властивості векторного добутку, отримаємо
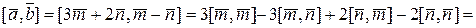
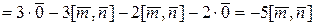 .
.
Тоді за означенням 

 . t
. t
Векторний добуток в координатній формі. Нехай в декартовій прямокутній системі координат задані вектори  ,
,  або, що те ж саме,
або, що те ж саме,  ,
,  .
.
Знайдемо векторний добуток цих векторів, перемноживши їх згідно властивостям 1–3:


 . (6.11)
. (6.11)
Векторні добутки  ,
,  ,
,  , що входять в цю рівність, рівні нульовому вектору згідно властивості 4.
, що входять в цю рівність, рівні нульовому вектору згідно властивості 4.
 |
Векторний добуток
 є вектором, модуль якого рівний
є вектором, модуль якого рівний  і колінеарний та однаково направлений з вектором
і колінеарний та однаково направлений з вектором  , а отже
, а отже  . Аналогічно
. Аналогічно  ,
,  (рис. 6.2). Згідно властивості 1
(рис. 6.2). Згідно властивості 1  ,
, 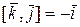 ,
,  .
.
Підставивши знайдені добутки в (6.11), отримаємо

 .
.
Цю рівність символічно можна записати у вигляді
 . (6.12)
. (6.12)
Приклад 6.9. Знайти  , якщо
, якщо  ,
,  .
.
Розв’язок. Згідно (6.12) отримаємо
 . t
. t
Приклад 6.10. Знайти площу трикутника  , якщо
, якщо  ,
,  ,
,  .
.
Розв’язок. Очевидно (рис. 6.2), що  . Так як
. Так як  ,
,  , то
, то
 |
 ,
,
 .
.
Отже,  . t
. t
Дата публикования: 2014-11-04; Прочитано: 819 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
