Побудова рекурентного співвідношення задачі 4.1.1

Дана задача, по суті, не є часовою. Але її можна звести до багатокрокового процесу прийняття рішень, якщо припустити, що різні продукти повинні вироблятися один за одним, тобто:

на першому кроці виробляється продукт 1,

на другому – продукт 2, …,

на 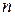-му – продукт .

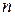Нехай вироблені продукти від 1-го до 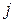-го включно і при цьому ресурс використаний у кількості 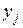. Дана ситуація описується за допомогою пари . Оскільки за умовою задачі ресурс споживається цілими порціями, то 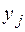є цілим числом і .

Позначимо через – максимальний прибуток, який можна отримати шляхом розподілу 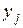одиниць ресурсу на виробництво продуктів з номерами від 1 до 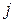включно. Будемо говорити, що виробництво одиниць 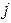-го продукту допустимо, якщо при цьому буде потрібно ресурсу не більше :

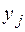і при цьому , - ціле.

Якщо - вироблена кількість продукту 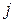, то ресурсу для цього використано і на виробництво продуктів 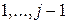пішло одиниць ресурсу. Тоді

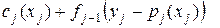(3)

є максимальним прибутком, який можна отримати від розподілу 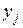одиниць ресурсу на виробництво продуктів з номерами від 1 до 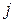включно за умови, що на кроці 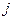вироблено одиниць продукту .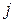

Ресурс, використаний на виробництво продуктів 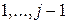, за визначенням функції , розподілений оптимально, тому сума (3) - це умовно максимальний прибуток.

Максимізуємо вираз (3) по допустимих значеннях

(4)

Вираз (4) справедливий і при 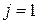, якщо покласти

Мета задачі – знайти .