Приклад застосування алгоритму АПП по дуга, що входять х

Алгоритмом прямої прогонки розв’яжемо ЗЗНШ для мережі, що представлена на рис. 10.

Оскільки при розв’язанні задачі застосовується пряма прогонка, то першим будемо планувати крок 1. Вважаємо, що .

Планування кроку 1.

Виділимо всі можливі стани, які можуть мати місце наприкінці кроку 1, тобто визначимо множину : . Для вершин знайдемо умовні оптимальні розв’язки , і відповідно. Тут – довжина найкоротшого шляху на кроці 1 (на кроках від 1-го до ( 1)-го включно), за умови, що наприкінці цього кроку система перебуває в стані (вершині) 2. Аналогічно визначаються й . Відповідно до виразу (2) отримаємо:

;

;

.

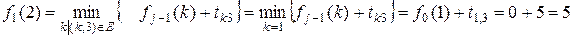!	У цьому випадку, у кожну вершину, що аналізується, входить тільки по одній дузі. Тому мінімум не шукається. У кожному випадку умовний оптимальний розв’язок відповідає переходу з вершини 1 (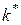 =1). Така ситуація завжди має місце, якщо в слої є тільки одна вершина (у нас – вершина 1).

Таблиця заповнюється таким чином:

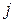
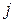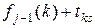
Крок	Можливі стани наприкінці кроку (вершини )	Варіанти розв’язків (управлінь) (попередня вершина)	Вартість розв’язку	Умовний оптимальний розв’язок
Вхідна дуга	Попередня вершина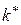
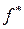
		a		0+2=2
	b		0+5=5
	c		0+3=3

У стовпчику 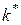вказується вершина 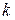, перехід з якої у вершину 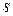забезпечує мінімум виразу (2). У стовпчику f^* вказується значення цього мінімуму – довжина найкоротшого шляху від вершини 1 до вершини .

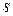Планування кроку 2.

Наприкінці цього кроку система може перебувати в одному з трьох станів (вершин): 5, 6 й 7. У стан 5 можна потрапити по дугах і (зі станів 2 й 3 відповідно). Тоді для стану 5 умовний оптимальний розв’язок знаходиться так:

,

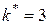– тобто, у вершину 5 найбільш вигідно можна потрапити з вершини 3.

У таблиці ці розрахунки відображаються таким чином:

		d		2+10=12
f		5+5=10

Для станів 6 і 7 співвідношення (2) мають вигляд:

,

– тобто, у вершину 6 найбільш вигідно можна потрапити з вершини 2.

, .

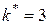Отже, частина таблиці, що відповідає етапу 2:

		d		2+10=12
f		5+5=10
	e		2+12=14
g		5+10=15
i		3+15=18
	h		5+7=12
j		3+13=16

Аналогічні дії виконуємо на кроках 3 і 4.

Повний процес розв’язання задачі наведений у таблиці 2:

Таблиця 2

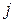
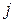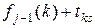
Крок	Можливі стани наприкінці кроку (вершини )	Варіанти розв’язків (управлінь) (попередня вершина)	Вартість розв’язку	Умовний оптимальний розв’язок
Вхідна дуга	Попередня вершина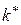
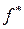
		a		0+2=2	1
3	b		0+5=5
	c		0+3=3
		d		2+10=12
f		5+5=10
	e		2+12=14
g		5+10=15
i		3+15=18
7	h		5+7=12	3
j		3+13=16
		k		10+7=17	5,6
m		14+3=17
p		12+7=19
9	l		10+5=15	7
n		14+4=18
q		12+1=13
	10	r		17+1=18	9
s		13+4=17

Порядок формування відповіді показано стрілками:

9→10

7→9→10

3→7→9→10

1→3→7→9→10

Відповідь: найкоротший шлях 1-3-7-9-10, довжина шляху 17.

3.6. Завдання для самостійної роботи

1. За допомогою алгоритма прямої прогонки, знайти найкоротший шлях між вершинами 1 і 9 мережі, зображеної на рис. 14.

Рис. 14

Відповідь: найкоротший шлях 1—2—6—7—9, довжина шляху 10.

2. За допомогою алгоритма прямої прогонки, знайти найкоротший шлях між вершиною A йоднієї з вершин останнього слою (вершинами G, H або I) наступної мережі (рис. 15).

Рис. 15

Відповідь: найкоротші шляхи: A—B—E—G; A—D—F—G; A—D—F—I, їх довжина 5.