Непрерывность функции. Определение 1. Функция называется непрерывной в точке , если она удовлетворяет следующим условиям

Определение 1. Функция 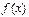называется непрерывной в точке 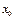, если она удовлетворяет следующим условиям:

1) определена в точке 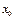, т.е. существует ;

2) имеет конечные односторонние пределы функции при слева и справа;

3) эти пределы равны значению функции в точке 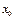, т.е.

.

Пример. Исследовать функции на непрерывность в точке :

а) , б) .

Решение. а) . При функция определена, 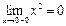, , 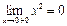, т.е. все три условия непрерывности функции в точке выполнены. Следовательно, функция в точке непрерывна.

б) . При функция не определена; ; .

Т.о. в точке функция не является непрерывной, т.к. не выполнены первое и третье условия непрерывности функции в точке.

Определение 2. Функция 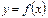называется непрерывной в точке 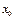, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: .

Определения 1 и 2 равносильны.

Точка 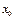называется точкой разрыва функции 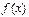, если эта функция в данной точке не является непрерывной. Различают точки разрыва:

Первого рода – когда существуют конечные односторонние пределы функции слева и справа при , не равные друг другу. К точкам разрыва первого рода относятся также точки устранимого разрыва, когда предел функции при существует, но не равен значению функции в этой точке.

Второго рода – когда хотя бы один из односторонних пределов слева или справа равен бесконечности или не существует.