Второй замечательный предел

Определение. Числом (вторым замечательным пределом) называется предел числовой последовательности :

, где

Прямым вычислением можно убедиться, что , (иррациональное число, число Эйлера).

Если рассмотреть функцию 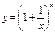, то при функция имеет предел, равный числу :

.

Или если , то .

Непосредственное вычисление этого предела приводит к неопределенности . Однако доказано, что он равен числу . Второй замечательный предел необходимо всегда использовать при раскрытии неопределенности вида .

Число (число Эйлера, неперово число) играет важную роль в математическом анализе. График функции

Рассмотрим примеры вычисления пределов. Получил название экспоненты. Широко используются логарифмы по основанию , называемые натуральными. Натуральные логарифмы обозначаются символом .

Пример. .

Пример. = .

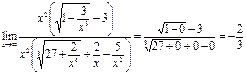Пример. .

Пример.

.

Пример. .

Пример. .

Пример. .