Предел числовой последовательности

Определение. Если по некоторому закону каждому натуральному числу поставлено в соответствие вполне определенное число , то говорят, что задана числовая последовательность :

.

Другими словами, числовая последовательность - это функция натурального аргумента: .

Числа называются членами последовательности, а число - общим или -м членом данной последовательности.

Примеры числовых последовательностей:

1) (монотонная, неограниченная),

2) (не монотонная, ограниченная)

3)

Рассмотрим числовую последовательность , изобразив ее точками на числовой оси (рис.4.1):

Видно, что члены последовательности с ростом как угодно близко приближаются к 0. При этом абсолютная величина разности становится все меньше и меньше.

Определение. Число 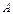называется пределом числовой последовательности , если для любого, даже сколь угодно малого положительного числа 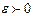, найдется такой (зависящий от 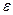), что для всех членов последовательности с номерами верно неравенство:

.

Обозначают: . Или при .

Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.