Метод простых итераций

Метод простых итераций (метод последовательных приближений) решения уравнения f(x) = 0 состоит в замене исходного уравнения эквивалентным ему уравнением x = j(x) и построении последовательности x_n+1 = j(x_n), сходящейся при n®¥ к точному решению. Сформулируем достаточные условия сходимости метода простых итераций [10].

Теорема. Пусть функция j(x) определена и дифференцируема на [a,b], причём все её значения j(x)Î[a,b]. Тогда, если существует число q, такое, что |j¢(x)| £ q < 1 на отрезке [a,b], то последовательность x_n+1 = j(x_n), n = 0, 1, 2, …, сходится к единственному на [a,b] решению уравнения x = j(x) при любом начальном значении x₀Î [a,b], т.е.

, , xÎ [a,b].

При этом, если на отрезке [a,b] производная j¢(x) положительна, то

,

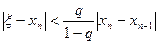если j¢(x) отрицательна, то

Опишем один шаг итераций. Исходя из найденного на предыдущем шаге значения x_n-1, вычисляем y = j(x_n-1). Если |y – x_n-1| > e, полагают x_n = y и выполняют очередную итерацию. Если же |y – x_n-1| < e, то вычисления заканчивают и за приближённое значение корня принимают величину x_n = y. Погрешность полученного результата зависит от знака производной j¢(x). При j¢(x) > 0 корень найден с погрешностью , если j¢(x) < 0, то погрешность не превышает e [10].

а) б)

Рис. 2.3.

Метод допускает простую геометрическую интерпретацию. Построим графики функций y = x и y = j(x). Корнем x уравнения x = j(x) является абсцисса точки пересечения кривой y = j(x) с прямой y = x (рис. 2.3). Взяв в качестве начальной произвольную точку x₀Î[a,b], строим ломаную линию (рис. 2.3, а, б). Абсциссы вершин этой ломаной представляют собой последовательные приближения корня x. Из рисунков видно, что если j¢(x) < 0 на отрезке [a,b], то последовательные приближения x_n = j(x_n-1) колеблются около корня x, если же производная положительна, то последовательные приближения сходятся к корню монотонно.

При использовании метода простых итераций основным моментом является выбор функции j(x) в уравнении y = j(x), эквивалентном исходному. Два метода итераций следует подбирать функцию j(x) так, чтобы |j¢(x)|£q<1. При этом следует помнить, что скорость сходимости последовательности {x_n} к корню x тем выше, чем меньше число q [10].