Метод Вегстейна

При выводе метода Вегстейна решения задачи о неподвижной точке x=φ(x) будем использовать как аналитические, так и геометрические соображения [1].

Пусть уже найдены: 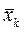- элемент строящейся здесь последовательности, и 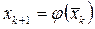- точка, соответствующая одному шагу МПИ, применённого к точке 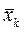. Независимо от того, сходится начатый с 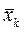МПИ (рис. 2.5, где 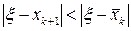) или расходится (рис. 2.6 с 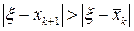), отрезок AB, параллельный оси Ox и имеющий концами точк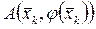и и 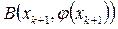, можно разделить точкой С так, чтобы она принадлежала прямой x = ξ (при этом во втором случае речь идёт о делении отрезка внешним образом) [1].

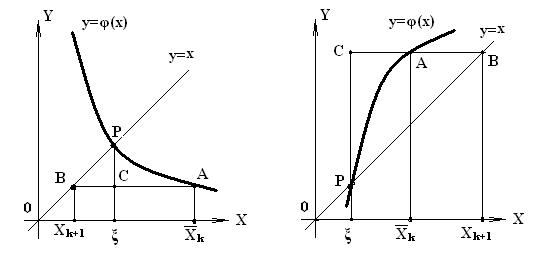
Рис. 2.5, 2.6. К построению метода Вегстейна.

При любых комбинациях направлений возрастания и выпуклости графика функции y=φ(x) в окрестности неподвижной точки ξ имеет место равенство длин отрезков BC = PC. Различаются два случая: когда 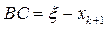и когда 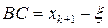. По формуле Лагранжа соответственно имеем

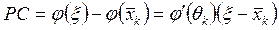
или

.

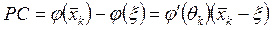В любом случае можно утверждать, что существует точка 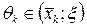или 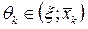такая, что

.

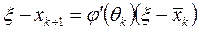Разрешая это линейное уравнение относительно ξ, находим

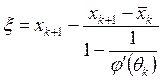. (2.12)

Если бы значение 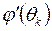было известно, то тем самым задача о неподвижной точке x=φ(x) была бы решена точно. Заменим это неизвестное значение 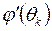аппроксимирующим его разностным отношением:

.

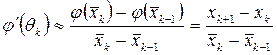Подставляя приближённое значение 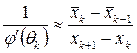в (2.12), вместо корня ξ получаем приближение к нему

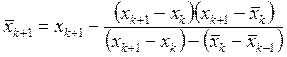. (2.13)

Эта итерационная формула, где k = 1,2,3,…, совместно с формулой

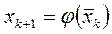(k = 0, 1, 2, …) (2.14)

и начальными значениями 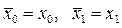полностью определяет метод Вегстейна для задачи x=φ(x) [1].

Значение 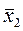, получаемое по формуле Вегстейна (2.13) при заданных начальных значениях 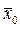и 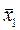, совпадает со значением 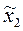, вычисляемым Δ² – процессом Эйткена. Далее, т.е. при k ≥ 2, процессы (2.11) и (2.13) различаются. Учитывая, что МПИ является составной частью метода Вегстейна, в случаях, когда 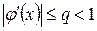, можно заканчивать процесс вычислений, как и в методе Эйткена.

Таким образом, для реализации метода может быть предложен, например, следующий алгоритм.