Число степеней свободы молекулы

Формула (31) определяет только энергию поступательного движения молекулы. Такой средней кинетической энергией обладают молекулы одноатомного газа. Для многоатомных молекул необходимо учесть вклад в кинетическую энергию, обусловленный вращением молекулы и колебанием атомов в молекуле.

Числом степеней свободы молекулы называется количество независимых координат, с помощью которых может быть однозначно задано положение молекулы в пространстве. Для одноатомной молекулы число степеней свободы = 3, это поступательные степени свободы , так как молекула рассматривается как материальная точка. В этом случае достаточно задать, например, три координаты точки относительно некоторой системы координат.

Если молекула многоатомная, но атомы в молекуле не могут смещаться друг относительно друга (молекулы с жесткой связью), то необходимо задать дополнительно еще две или три координаты, чтобы определить ориентацию молекулы в пространстве (например, задать углы, которые образует молекула с осями координат), эти степени свободы называются вращательными - . Для двухатомной или любой линейной многоатомной молекулы (например –СО₂) =2, для многоатомной нелинейной молекулы =3. Если атомы в молекуле могут совершать колебания (молекулы с нежесткой связью), то для однозначного определения положения молекулы необходимо знать координаты всех N атомов, входящих в молекулу. Полное число степеней свободы в этом случае равно 3N, число колебательных степеней свободы, таким образом, равно .

Число степеней свободы для различных молекул представлено в таблице 4.2.1:

Таблица 4.2.1.

Число атомов в молекуле (N)	Число степеней свободы
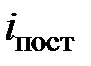
			Полное число степеней свободы
		-	-
3(нелинейная молекула)
3(линейная молекула)
(нелинейная молекула)			3N-6	3N
(линейная молекула)			3N-5	3N