Распределение молекул по скоростям

Опыт показывает, что скорости молекул газа, который находится в равновесном состоянии, могут иметь самые разные значения – и очень большие, и близкие к нулю. Скорость молекул может принимать любые значения от 0 до некоторого значения . Это происходит вследствие многочисленных случайных столкновений молекул друг с другом и обмена энергиями. Скорость молекулы – непрерывная случайная величина. Но неправомерно ставить вопрос, какова вероятность того, что скорость молекулы равна, например, 110,25 м/с. Если бы была возможность одновременно и совершенно точно измерить скорости всех молекул в данном объеме газа, то среди них не нашлось бы молекулы точно с такой скоростью, но были бы молекулы, со скоростями, близкими к этому значению. Таким образом, можно говорить лишь о вероятности 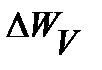того, что величина скорости молекулы лежит в некотором интервале [ ]. Эту вероятность можно определить так же, как это делалось в предыдущем примере с шарами:

, (4.2.2)

где - число молекул, величина скорости которых лежит в указанном выше интервале, N – общее число молекул газа.

Очевидно, что должна зависеть от величины (чем больше , тем большее число молекул имеют скорости, попадающие в этот интервал) и от самого значения скорости V.

Отложим интервал возможных значений скорости [ 0, ] на оси абсцисс. Разобьем весь интервал на отрезки, шириной V. На этих отрезках построим столбики, высота которых равна 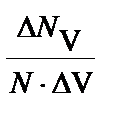, что представляет собой плотность вероятности нахождения молекул в интервале скоростей . Полученная столбчатая диаграмма, называется гистограммой (рис. 4.2.1. а), она дает наглядное представление о распределении молекул по скоростям. Площадь каждого столбика будет равна . Полная площадь гистограммы, в соответствии с условием нормировки, равна единице:

, (4.2.3)

что физически означает равенство единице полной вероятности W нахождения молекул во всем интервале скоростей – от нуля до бесконечности.

Здесь - есть число молекул, движущихся со скоростью V, лежащей в интервале значений , а - есть относительное число молекул, обладающих скоростью V в указанном выше интервале скоростей.

Рис. 4.2.1 а. Гистограмма распределения молекул по скоростям

В пределе при ∆v→ 0 огибающая столбиков превращается в гладкую кривую (рис. 4.2.1 б), которую можно задать аналитически в виде функции F (V). Эта функция носит название плотности вероятности распределения молекул по скоростям, или просто функции распределения молекул по скоростям. Тогда вероятность того, что величина скорости молекулы лежит в интервале [V; V +d V], равна

(4.2.4)

и определяется площадью заштрихованной фигуры, представленной на рис. 4.2.1 б.

.

Рис. 4.2.1 б. График функции распределения молекул по скоростям.

С другой стороны, равна относительному числу молекул, скорости которых лежат в указанном выше интервале:

,

где число молекул, скорости которых лежат в интервале [V, V+dV].

По аналогии с условием нормировки (4.2.3) полная площадь фигуры на рис. 4.2.1 б, ограниченной осями координат и кривой F( V ), имеет смысл полной вероятности и равна единице:

(4.2.5)

Функция распределения F (V) молекул газа по абсолютным значениям скоростей была получена Дж. К. Максвеллом и является справедливой для идеального газа, состоящего из одинаковых частиц, находящегося в состоянии равновесия, в отсутствие внешних силовых полей. В этом случае температура, концентрация, давление имеют одинаковое по всей системе значение. Аналитически функция F (V) задается следующим выражением:

, (4.2.6)

где константа С находится из условия нормировки (4.2.6).

Выражение для функции распределения F (v) справедливо во всем диапазоне скоростей от нуля до бесконечности. Вид этой функции представлен на рис. 4.2.2.

Рис. 4.2.2. График функции Максвелла для распределения молекул по скоростям.

Поскольку при возрастании скорости v множитель вида убывает быстрее, чем растет множитель , функция F (v), начинаясь в нуле (из-за ), достигает максимума и затем асимптотически стремится к нулю. Площадь, охватываемая кривой, равна единице – в соответствии с условием нормировки (4.2.5).

После подстановки выражения (4.2.6) в условие нормировки получим

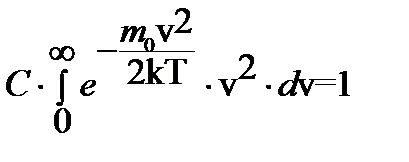. (4.2.7)

Вычислим интеграл и получим выражение для константы С:

(4.2.8)

С учетом этого результата функцию Максвелла – функцию распределения молекул по скоростям можно записать в следующем виде:

(4.2.9)

Рис. 4.2.3. Вид функции при различных температурах

При увеличении температуры максимум функции, в соответствии с формулой (4.2.25), сдвигается в сторону больших значений скорости, а сам максимум становится ниже, поскольку, в соответствии с условием нормировки (4.2.5), площадь под кривой остается постоянной и равной единице.

В формулах (4.2.8) и (4.2.9) отношение иногда удобнее заменить отношением 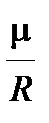, что удобнее, так как молярную массу газа можно определить без труда в соответствии с формулами (4.1.2)…(4.1.4): ,

где m ₀ - масса одной молекулы , а постоянная Больцмана k связана с универсальной газовой постоянной R соотношением:

(4.2.10)

Умножив соответствующую вероятность на полное число молекул газа , получим число молекул , модуль скорости которых лежит в указанном выше узком интервале значений величин скоростей. Чтобы найти число молекул , модуль скорости которых лежит в пределах значений от до , необходимо провести интегрирование:

.

Рис. 4.2.4. График функции Максвелла с указанием наиболее вероятной, средней и средней квадратичной скоростей.

Функция Максвелла (рис. 4.2.4.) имеет максимум при значении скорости

, (4.2.11)

которое вычисляется из условия и называется наиболее вероятной скоростью.

Средняя скорость молекул определяется по формуле: . (4.2.12).

среднее значение квадрата скорости найдем по формуле:

.(4.2.13)

Средней квадратичной скоростью называется величина

. (4.2.14)