 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Электрический колебательный контур. Формула Томсона
|
|
Электромагнитные колебания могут возникать в цепи, содержащей индуктивность L и емкость C (рис.16.1). Такая цепь называется колебательным контуром. Возбудить колебания в таком контуре можно, например, предварительно зарядив конденсатор от внешнего источника напряжения, соединить его затем с катушкой индуктивности.
| С |
| L |
Рис.16.1. Электрический колебательный контур.
Поскольку внешнее напряжение к контуру не приложено, сумма падений напряжений на емкости и индуктивности должна быть равна нулю в любой момент времени:
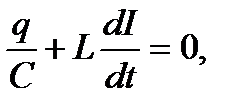
откуда, учитывая, что сила тока 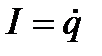 , получаем дифференциальное уравнение свободных незатухающих колебаний электрического заряда в колебательном контуре
, получаем дифференциальное уравнение свободных незатухающих колебаний электрического заряда в колебательном контуре
 .
.
Если ввести обозначение
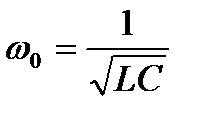 ,
,
то полученное уравнение принимает вид:
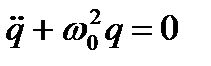 .
.
Решением этого уравнения, как известно, является функция
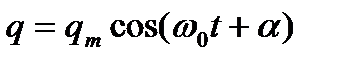 .
.
Таким образом, заряд на обкладках конденсатора изменяется по гармоническому закону с частотой ω0, называемой собственной частотой колебательного контура. Период колебаний определяется по формуле Томсона (Thomson W., 1824-1907):

Напряжение на конденсаторе:
 ,
,
где 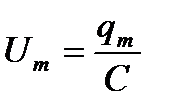 - амплитуда напряжения.
- амплитуда напряжения.
Сила тока в контуре:
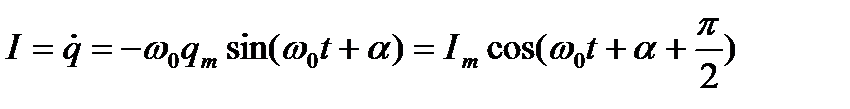 .
.
Сопоставляя полученные выражения, видим, что когда напряжение на конденсаторе, а значит энергия электрического поля, обращается в нуль, сила тока, а, следовательно, энергия магнитного поля, достигает максимального значения (рис.16.2). Таким образом, электрические колебания в контуре сопровождаются взаимными превращениями энергий электрического и магнитного полей.
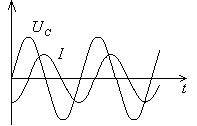
Рис.16.2. Графики изменения UC(t) и I(t) в LC-контуре.
Амплитуды тока Im и напряжения Um связаны между собой очевидным соотношением:
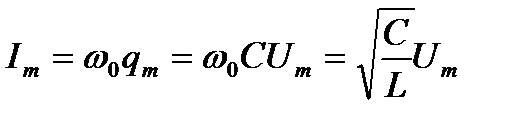 .
.
Дата публикования: 2014-11-04; Прочитано: 4073 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
