Дифференциальная форма уравнений Максвелла

1. Применяя теорему Стокса, преобразуем левую часть первого уравнения Максвелла к виду: .

Тогда само уравнение можно переписать как , откуда, в силу произвольности поверхности интегрирования, имеем:

2. Применяя теорему Остроградского ко второму уравнению Максвелла, находим:

,

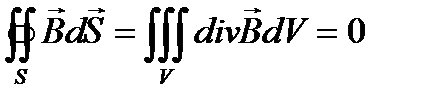откуда, в силу произвольности объема интегрирования, имеем:

3. Применяя теорему Стокса, преобразуем левую часть третьего уравнения Максвелла к виду:

.

Тогда само уравнение можно переписать как , откуда, в силу произвольности поверхности интегрирования, имеем:

4. Применяя теорему Остроградского, преобразуем левую часть четвертого уравнения Максвелла к виду:

.

Тогда само уравнение можно переписать как , откуда, в силу произвольности объема интегрирования, имеем: