Следствия из уравнений Максвелла. Электромагнитные волны. Скорость света

Рассмотрим некоторые основные следствия, вытекающие из уравнений Максвелла, приведенных в таблице 2. Прежде всего, отметим, что эти уравнения линейные. Отсюда следует, что электромагнитное поле удовлетворяют принципу суперпозиции.

Одним из главных следствий, вытекающих из уравнений Максвелла, является то, что электромагнитное поле может существовать в виде электромагнитных волн в отсутствие всяких зарядов и токов ().

В этом случае уравнения Максвелла принимают вид (в дифференциальной форме):

Применяя к первому из этих уравнений операцию , будем иметь:

.

Но согласно третьему уравнению (с учетом материальных уравнений): . Используя это соотношение, получим:

.

Далее, принимая во внимание, что , причем в силу четвертого уравнения , приходим к так называемому волновому уравнению для электрического поля :

где обозначено - оператор Лапласа (в декартовых координатах).

Аналогичное волновое уравнение получается для магнитного поля :

Совместным решением этих уравнений является векторная волновая функция электромагнитного поля:

, .

Коэффициент имеет смысл фазовой скорости электромагнитной волны (см. Лекцию 17):

Для вакуума: . Тогда: м/c, что совпадает со скоростью света в вакууме с. Таким образом, мы приходим к выводу, что свет – это электромагнитная волна.

В прозрачной диэлектрической среде скорость света

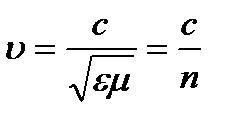
где величина называется показателем преломления среды. Для многих оптически прозрачных сред эта формула дает хорошие совпадения с измеренными на опыте значениями n, что также является одним из достижений теории Максвелла.