Замкнутая система уравнений Максвелла. Материальные уравнения

Для замыкания системы уравнений Максвелла необходимо еще указать связь между векторами , , и , то есть конкретизировать свойства материальной среды, в которой рассматривается электромагнитное поле. Если эти соотношения известны (они называются материальными уравнениями), то по заданному распределению зарядов ρ и токов однозначно находится распределение электрических и магнитных полей в данной среде; или по заданному распределению полей находится распределение зарядов и токов. Для однородной изотропной среды материальные уравнения записывают обычно в виде:

; .

Если среда не обладает сегнетоэлектрическими или ферромагнитными свойствами, то и . В этом случае материальные уравнения имеют наиболее простой вид:

;

(в частности, для вакуума , тогда и ).

Следует подчеркнуть, что написанные соотношения справедливы только для неподвижных сред. В движущихся средах они имеют более сложный вид, обусловленный требованиями релятивистской инвариантности уравнений Максвелла.

Таблица 2. Замкнутая система уравнений Максвелла.

Интегральная форма	Дифференциальная форма
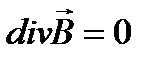
Материальные уравнения