Пружинный маятник. В соответствии со вторым законом Ньютона:

В соответствии со вторым законом Ньютона:

,
, (2.2.17)

где

(2.2.18)

– внешняя периодическая сила, действующая на пружинный маятник.

В скалярном виде:

.(2.2.19)

Дифференциальное уравнение вынужденных колебаний пружинного маятника:

можно представить в виде

,(2.2.20)

где (2.2.21) – приведенная сила.

2.2.2.2.Решение дифференциального уравнения вынужденных колебаний (на примере пружинного маятника)

В колебательной системе одновременно происходят два процесса:

1. Затухающие колебания x ₁(t);

2. Незатухающие вынужденные колебания x ₂(t) с частотой вынуждающей силы.

Решение дифференциального уравнения вынужденных колебаний (2.2.20)

представим в виде суммы двух решений

x = x ₁ + x ₂:

1. Общее решение однородного уравнения затухающих колебаний:

,(2.2.21)

где – циклическая частота затухающих колебаний.

2. Частное решение неоднородного уравнения вынужденных колебаний:

,(2.2.22)

где y(w) – начальная фаза вынужденных колебаний.

Подставим x ₂ в исходное дифференциальное уравнение и получим:

.(2.2.23)

Для использования метода векторной диаграммы представим это уравнение в виде:

.(2.2.24)

Из этого уравнения следует, что постоянные А и должны иметь такие значения, чтобы гармоническая функция f ₀ cos wt была равна сумме трех гармонических функций, стоящих в левой части этого уравнения.

Представим (рис. 2.2.4 а, б):

– функцию вектором ;

– функцию вектором , повернутым относительно вектора на угол (–y);

– функцию вектором , повернутым на угол относительно вектора ;

– функцию вектором , повернутым относительно вектора на угол p.

Рис. 2.2.4. Векторные диаграммы для решения дифференциального уравнения вынужденных колебаний: а) w < w₀ и б) w > w₀

Чтобы рассматриваемое уравнение было удовлетворено, должно выполняться следующее векторное равенство

.(2.2.25)

Векторные диаграммы, соответствующие случаям w < w₀ и w > w₀, представлены на рис. 2.2.4, а, б.

Из этих диаграмм следует, что уравнение справедливо, если

и при w < w₀ (2.2.26)

и

и при w > w₀. (2.2.27)

Резонансом называют явление резкого увеличения амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте собственных колебаний (w ® w₀).

При w ® w₀ tgy ® ¥ и начальная фаза y стремится к 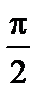, то есть вектор внешней силы становится параллельным вектору скорости маятника.

A = A (w) – амплитудно-частотная характеристика (резонансная кривая) представлена на рис. 2.2.5.

Рис. 2.2.5. Амплитудно-частотная характеристика вынужденных колебаний: A _рез– резонансная амплитуда, A _стат – статическая амплитуда

Функция A (w) достигает экстремума при частоте вынуждающей силы w, равной

, (2.2.28)

здесь w_рез – резонансная частота.

Если w ® 0, то

, (2.2.29)

здесь A _стат – статическая амплитуда.

при w ® ¥ амплитуда вынужденных колебаний A ® 0.

При достижении резонансной частоты

w ® w_рез

амплитуда стремится к резонансной величине

,(2.2.30)

здесь A _рез – резонансная амплитуда.

Семейство резонансных кривых при различных коэффициентах затухания представлено на рис. 2.2.6.

Рис. 2.2.6. Амплитудно-частотные характеристики при различных коэффициентах затухания

При критическом затухании

(2.2.31)

резонанс не наступает – резонансная частота w_рез стремится к нулю.

Добротность колебательной системы, находящейся в режиме вынужденных колебаний, можно найти как

,(2.2.32)

где Dw_0,7 – ширина резонансной кривой (рис. 2.2.7) на уровне половинной мощности внешнего источника вынуждающей силы

.

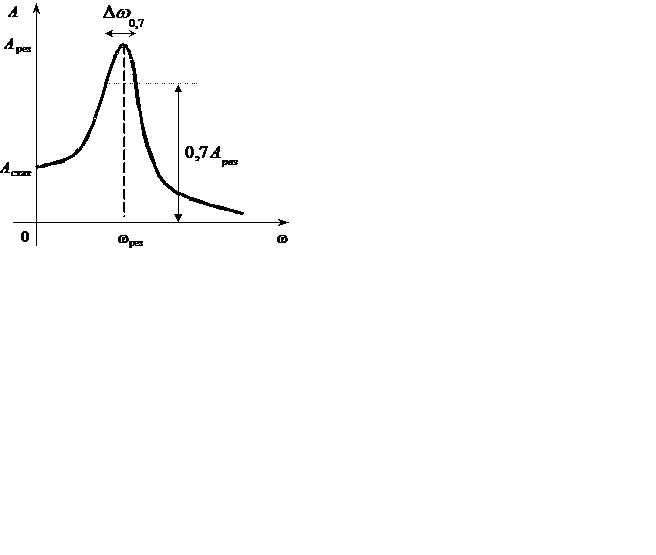
Рис. 2.2.7. Определение величины добротности

Добротность можно представить и как отношение резонансной амплитуды к статической, т.е. как коэффициент усиления:

.(2.2.33)

При слабом затухании добротность равна

.(2.2.34)