Пружинный и физический (математический) маятники

Для произвольных колебательных систем дифференциальное уравнение собственных колебаний имеет вид:

.(2.1.43)

Зависимость смещения от времени (рис. 2.1.7)

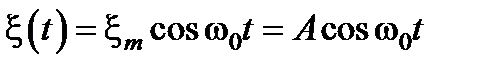.(2.1.44)

при условии, что начальная фаза j = 0.

Рис. 2.1.7. Графики зависимости смещения x и потенциальной энергии U от времени t

Поскольку потенциальная энергия ЛГО пропорциональна квадрату смещения осциллятора из положения равновесия, то зависимость потенциальной энергии от времени (см. рис. 2.1.7): .(2.1.45)

Поскольку зависимость скорости колебания от времени (рис. 2.1.8)

,(2.1.46)

а кинетическая энергия ЛГО пропорциональна квадрату скорости, то зависимость кинетической энергии от времени (см. рис. 2.1.8):

.(2.1.47)

Поскольку зависимость ускорения ЛГО от времени (рис. 2.1.9)

,(2.1.48)

а возвращающая сила пропорциональна ускорению

,(2.1.49)

то график зависимости возвращающей силы от времени будет аналогичен графику ускорения (см. рис. 2.1.10).

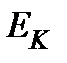
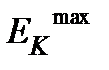
Рис. 2.1.8. Графики зависимости скорости колебания 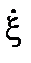и кинетической энергии K от времени t

Рис. 2.1.9. Графики зависимости ускорения и
возвращающей силы F от времени t

Так же будет выглядеть и график зависимости от времени момента возвращающей силы, действующей на физический (математический) маятник