Физический маятник. Уравнение основного закона динамики вращательного движения абсолютно твердого тела:

Уравнение основного закона динамики вращательного движения абсолютно твердого тела:

.(2.1.33)

Так как для физического маятника (рис. 2.1.6) , то

.

При малых углах sinq» q (в радианах). Тогда:

.(2.1.34)

дифференциальное уравнение собственных колебаний физического маятника:

.(2.1.35)

Рис. 2.1.6. Динамика физического маятника:
¤ – вектор момента силы тяжести относительно точки О;
Ä – вектор угла поворота

Поскольку 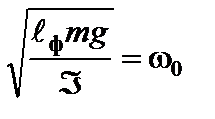(2.1.15)– собственная циклическая частота колебаний, то дифференциальное уравнение собственных колебаний физического маятника:

.(2.1.36)

Для математического маятника дифференциальное уравнение собственных колебаний:

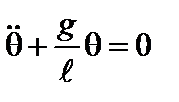,(2.1.37)

где 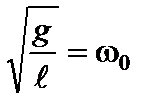– собственная циклическая частота (2.1.18).

Тогда дифференциальное уравнение собственных колебаний математического маятника тоже можно представить в виде:

.(2.1.38)