Пружинный маятник

Закон сохранения и превращения энергии колебаний пружинного маятника (рис. 2.1.2):

Е_Р^max = Е_Р + E_K = E_K^max, (2.1.3)

где Е_Р^max и E_K^max – амплитудные значения потенциальной и кинетической энергий, соответственно.

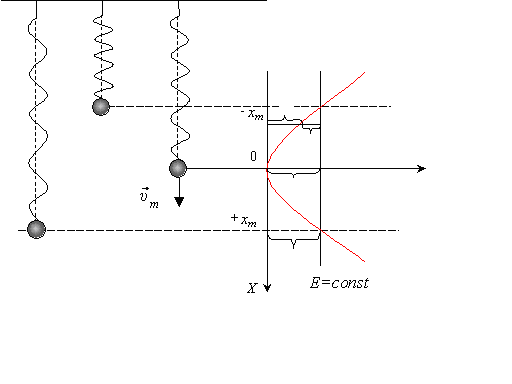
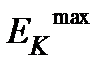
Рисунок 2.1.2. Энергетика колебаний пружинного маятника

При малых отклонениях от положения равновесия изменением потенциальной энергии материальной точки в однородном поле тяготения можно пренебречь.

Рассмотрим превращение энергии за половину периода колебания:

,(2.1.4)

где , x – мгновенное значение отклонение маятника от положения равновесия, а x_{m –} максимальное значение этого отклонения.

Отсюда

.

После разделения переменных и интегрирования получаем:

,

откуда

.(2.1.5)

Если в начальный момент времени t = 0 смещение x ₀ = , то и решение интегрального уравнения имеет вид:

.(2.1.6)

Амплитуда определяется начальным запасом энергии и не зависит от параметров колебательной системы.

Собственная циклическая (круговая) частота зависит от параметров колебательной системы:

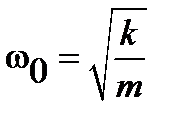.(2.1.7)

Период собственных колебаний: T ₀.

Линейная частота: n₀.

Фаза колебания: Ф = w₀ t определяет значение смещения х в данный момент времени.

Если в момент времени t = 0 смещение , то фаза колебания

Ф = w₀ t + j,(2.1.8)

где j – начальная фаза колебания.

уравнение гармонических колебаний пружинного маятника:

.(2.1.9)