Пружинный маятник. Уравнение основного закона динамики поступательного движения материальной точки (второй закон Ньютона):

Уравнение основного закона динамики поступательного движения материальной точки (второй закон Ньютона):

.(2.1.28)

Пружинный маятник в положении равновесия (рис. 2.1.5):

или mg – kx ₀ = 0.

Отсюда

Þ .(2.1.29)

Рис. 2.1.5. Динамика пружинного маятника

При смещении маятника из положения равновесия возникает возвращающая упругая сила

.

Отсюда

. (2.1.30)

дифференциальное уравнение собственных колебаний пружинного маятника:

.(2.1.31)

Поскольку 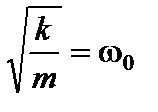– собственная циклическая частота колебаний пружинного маятника (2.1.7), то дифференциальное уравнение собственных колебаний можно представить в виде:

.(2.1.32)