Физический смысл потока

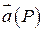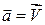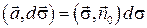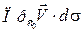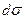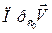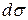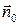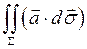Пусть - поле скоростей некоторой жидкости , а - произвольная поверхность в поле, тогда: = = - объём столба жидкости с основанием и высотой , т.е. объем жидкости, протекающей через площадку в единицу времени в направлении . Суммируя по поверхности , получаем, что - поток жидкости, протекающей через поверхность в единицу времени.

ПРИМЕР. Вычислить поток векторного поля радиус-вектора 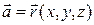через внешнюю сторону цилиндра (H – высота, R - радиус).

Решение:

;_,

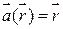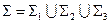
следовательно,

.

= =…

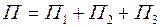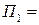
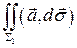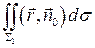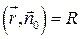{ , из рисунка ясно, что проекция 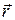на нормаль к равна R}

…= .

= = …

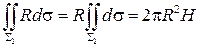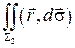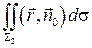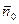{из рисунка ясно, что проекция на по 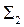равна H,
т.е. }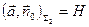

…= .

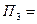
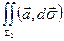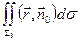= =0.

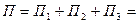3 pR²H.

ПРИМЕР. Вычислить поток векторного поля 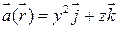через всю поверхность (нормаль внешняя): .

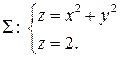Решение:

Разобьем поверхность на две части 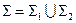и представим поток в виде ;

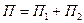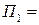
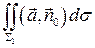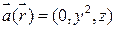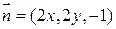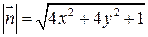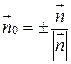= , ; , , (знак выбирается «+», так как ), .

= =…

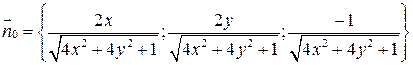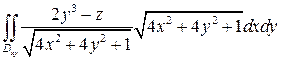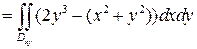{перейдем в полярную систему координат}

.

=

{ }

= .

.

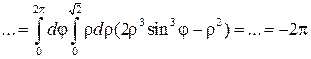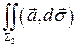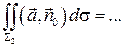
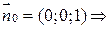
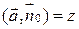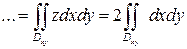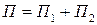
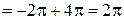ПРИМЕР. Найдите поток вектора 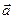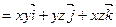через часть сферы 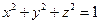, расположенную в первом октанте (нормаль внешняя).

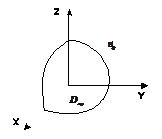Решение:

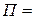
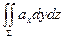
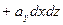
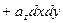
{компоненты поля и области интегрирования обладают симметрией относительно замены 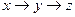и }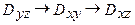

= .

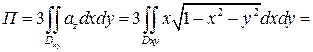
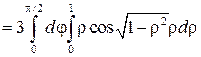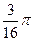Важно отметить, что cosα, cosβ, cosγ положительны, перед всеми интегралами берется знак (+), так как сторона поверхности - внешняя.