 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Плотность распределения вероятностей
|
|
Определение 1. Дифференциальной функцией распределения или плотностью распределения вероятностей называется первая производная интегральной функции распределения 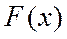 .
.
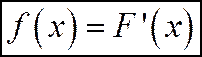
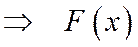 - первообразная для
- первообразная для 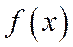
Плотность распределения вероятностей 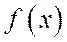 , как и функция распределения
, как и функция распределения 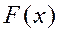 , является одной из форм закона распределения, но в отличие от функции распределения она существует только для непрерывных случайных величин, поскольку для существования
, является одной из форм закона распределения, но в отличие от функции распределения она существует только для непрерывных случайных величин, поскольку для существования 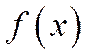 требуется непрерывность и дифференцируемость функции
требуется непрерывность и дифференцируемость функции 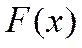 , а для дискретной случайной величины эти требования не выполняются.
, а для дискретной случайной величины эти требования не выполняются.
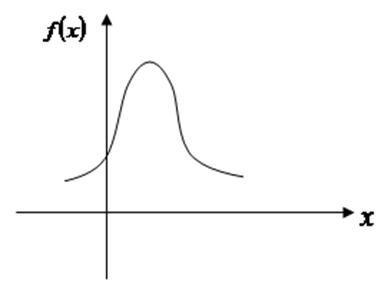
График плотности распределения 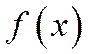 называется кривой распределения.
называется кривой распределения.
Свойства плотности распределения вероятностей.
1. Для любых Х дифференциальная функция распределения 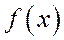 неотрицательна, т.е.
неотрицательна, т.е. 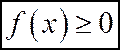
2. Для интегральной и дифференциальной функции распределения имеет место равенство:
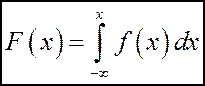
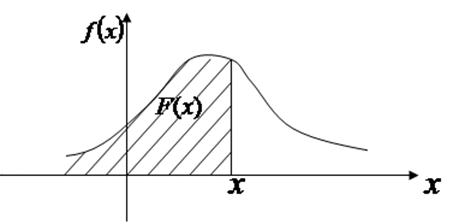
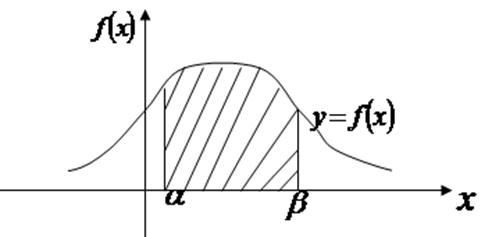
3. Вероятность того, что случайная величина Х примет значение из интервала 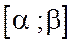 равна определенному интегралу от ее плотности вероятности в пределах от α до β
равна определенному интегралу от ее плотности вероятности в пределах от α до β
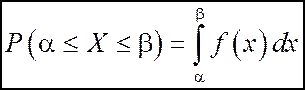
С геометрической точки зрения, вероятность попадания случайной величины в интервал 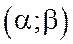 численно выражается площадью криволинейной трапеции, ограниченной сверху кривой
численно выражается площадью криволинейной трапеции, ограниченной сверху кривой 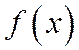 , снизу - осью ОХ
, снизу - осью ОХ 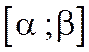 , слева и справа прямыми
, слева и справа прямыми 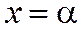 и
и 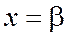
4. Несобственный интеграл в бесконечных пределах от плотности распределения вероятностей равен 1.
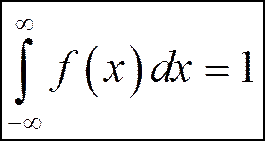
Дата публикования: 2014-11-04; Прочитано: 465 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
