 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Непрерывную случайную величину можно задать еще с помощью функции
|
|
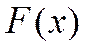 - функции распределения вероятностей случайной величины.
- функции распределения вероятностей случайной величины.
Определение 1. Функцией распределения (интегральной функцией распределения) называется вероятность того, что случайная величина Х примет значения в результате испытания меньше, чем х
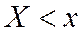 , т.е.
, т.е. 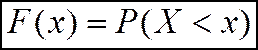
Свойства функции 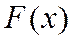
Т.к. 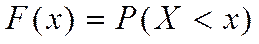 , то
, то
1. 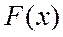 неотрицательная:
неотрицательная: 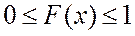
2. 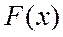 - неубывающая, т.к. для
- неубывающая, т.к. для 
3. Если все возможные значения случайной величины находятся в промежутке 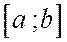 , то при
, то при 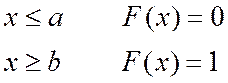
4. Вероятность того, что случайная величина примет значение, заключенное в интервале 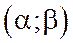 будет равна:
будет равна:
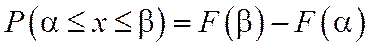
5. 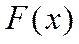 - универсальная характеристика случайной величины, так как она существует и для непрерывной, и для дискретной случайной величины.
- универсальная характеристика случайной величины, так как она существует и для непрерывной, и для дискретной случайной величины.
Для непрерывной случайной величины. – график 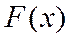 непрерывная линия.
непрерывная линия.
Для дискретной случайной величины – график 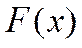 имеет ступенчатый вид.
имеет ступенчатый вид.
Свойства функции 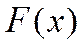 дают представления о графике этой функции:
дают представления о графике этой функции:
1. График расположен в полосе, ограниченной прямыми 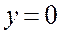 и
и 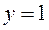 (1-е свойство)
(1-е свойство)
2. при  ординаты графика = 0
ординаты графика = 0
при 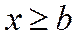 ординаты графика = 1
ординаты графика = 1
Построим функцию распределения случайной величины Х, закон распределения которой представлен таблицей:
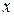
| 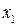
| 
| 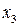
| … | 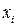
| … | 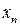
|
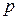
| 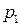
| 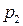
| 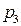
| … | 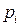
| … | 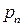
|
при 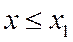
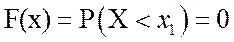
при 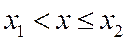

при 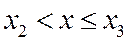
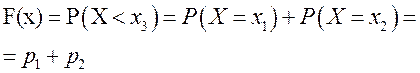
при 
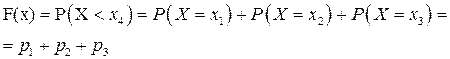
при 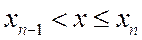
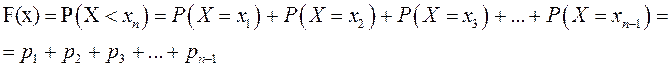
при 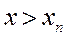
Для дискретной случайной величины график функции распределения представляет собой разрывную ступенчатую линию. Когда переменная х проходит через какое-нибудь из возможных значений случайной величины, значение функции распределения меняется скачкообразно, т.е. функция имеет скачок в тех точках, в которых случайная величина принимает конкретное значение согласно закону распределения, причем величина скачка равна вероятности этого значения. Сумма величин всех скачков функции распределения равна 1. В интервалах между значениями случайной величины функция 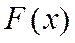 постоянна.
постоянна.
Пример 1: Дана дискретная случайная величина х, заданная законом распределения. Найти функцию распределения и построить ее график.
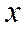
| |||
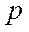
| 0,3 | 0,1 | 0,6 |
при 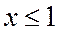
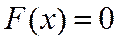
при 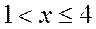
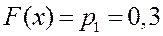
при 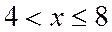
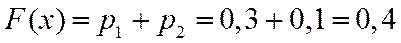
при 
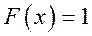
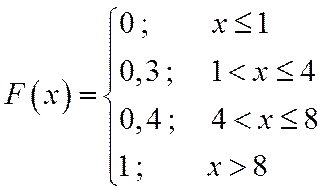
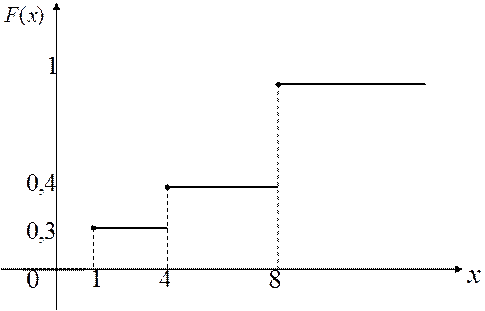

Пример 2: Построить график функции распределения и найти вероятность того, что случайная величина примет значение из интервала 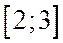
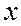
| ||
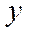
| -1 |
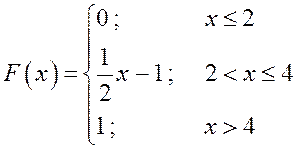
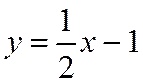
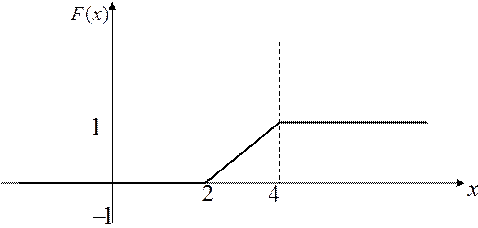

при 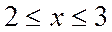
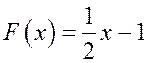
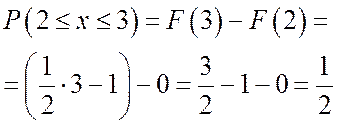
Дата публикования: 2014-11-04; Прочитано: 412 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
